Представление Пуассона для гармонических функций, принадлежащих некоторым классам
Пусть известно лишь, что функция U(z) гармонична в круге {|z| < 1}. Замечательно, что часто её всё же можно представить в этом круге по формуле Пуассона.
Теорема. Пусть р > 1, и пусть V (г) — гармоническая функция в {\z\ < 1}. Предположим, что средние
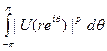
ограничены при r<.1. Тогда существует такая функция 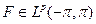 , что
, что
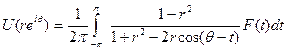
для г < 1, 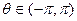
Доказательство.
При р > 1 пространство 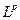 является cопряжённым с
является cопряжённым с  , где
, где 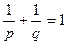 . Для функций
. Для функций 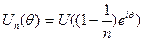 (вместо
(вместо 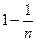 подходит любая последовательность
подходит любая последовательность 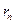 , стремящаяся к 1 снизу) имеем
, стремящаяся к 1 снизу) имеем 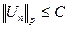 (
( 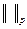 здесь, конечно, берётся по отрезку (—π,π)), так что канторовским диагональным процессом мы можем выделить из них подпоследовательность Unh такую что для всех функций G, пробегающих некоторое счётное всюду плотное подмножество пространства
здесь, конечно, берётся по отрезку (—π,π)), так что канторовским диагональным процессом мы можем выделить из них подпоследовательность Unh такую что для всех функций G, пробегающих некоторое счётное всюду плотное подмножество пространства  , существует предел
, существует предел
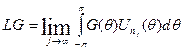
Так как 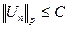 , то этот предел LG на самом деле существует для всех
, то этот предел LG на самом деле существует для всех 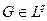 и LG является ограниченным линейным функционалом на Lq. Следовательно, поскольку пространство Lp сопряжено с Lq, то существует такая функция
и LG является ограниченным линейным функционалом на Lq. Следовательно, поскольку пространство Lp сопряжено с Lq, то существует такая функция 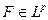 , что
, что
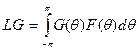
всех 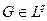 .
.
Теперь, для каждого п функция 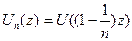 гармонична в
гармонична в 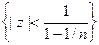 , так что если r < 1, то
, так что если r < 1, то
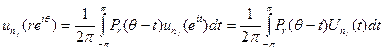
Зафиксируем произвольное r <. 1 и любое θ и возьмём G (t) = 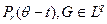 . Тогда
. Тогда
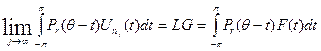
В этом равенстве слева стоит
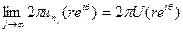
Таким образом,
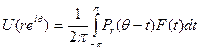 ,
,
где 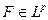
Замечание Тот же результат справедлив с тем же доказательством и при р =∞, если мы немного изменим формулировку теоремы:
Теорема. Если U(z) — ограниченная гармоническая функция в {|z| < 1}, то существует функция 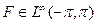 , такая что
, такая что
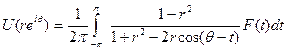
А что же в случае р=1? Пространство 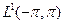 , к сожалению, не является сопряжённым ни с каким другим. Но М — пространство конечных вещественных мер μ на [-π, π] с нормой ||μ||, равной полной вариации меры μ,— сопряжено с С [-π, π] —пространством непрерывных функций на [-π, π]. Если
, к сожалению, не является сопряжённым ни с каким другим. Но М — пространство конечных вещественных мер μ на [-π, π] с нормой ||μ||, равной полной вариации меры μ,— сопряжено с С [-π, π] —пространством непрерывных функций на [-π, π]. Если 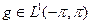 , то мы можем связать с g меру μ, положив
, то мы можем связать с g меру μ, положив
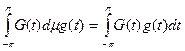
при этом 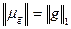 .
.
Теперь рассуждение, проведенное при доказательстве первой теоремы этого пункта, показывает, что справедлива такая
Теорема. Если U(z)—гармоническая функция в круге {|z|< 1} и средние
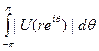
ограничены при r< 1, то существует конечная вещественная мера μ на [-π, π], такая что
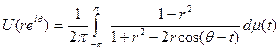
для 0≤r< 1.
Следствие (Званс). Пусть U(z)-функция, гармоническая и положительная (здесь и далее «положительный» означает «неотрицательный») в круге {|z|<1}. Тогда существует конечная положительная мера μ на [-π, π],, такая что
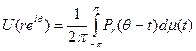
Доказательство.
Для r<1 (используя, например, разложение 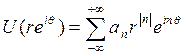 , имеющее место в {|z| < 1}) получаем
, имеющее место в {|z| < 1}) получаем
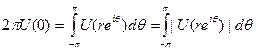 ,
,
гак как 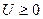 . А теперь применяем теорему. Мера μ положительна, потому что в этом случае (см. опять доказательство первой теоремы этого пункта) оказывается, что интеграл
. А теперь применяем теорему. Мера μ положительна, потому что в этом случае (см. опять доказательство первой теоремы этого пункта) оказывается, что интеграл 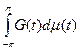 положителен для любой положительной функции
положителен для любой положительной функции 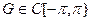 как предел положительных чисел!
как предел положительных чисел!
Дата добавления: 2015-08-14; просмотров: 684;
