Представление в виде степенного ряда
Лекция № 1, 2
Пусть U(z) – вещественная функция, гармоническая в круге 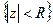 . Тогда можно построить другую вещественную функцию V(z) , гармоническую в
. Тогда можно построить другую вещественную функцию V(z) , гармоническую в 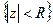 , такую что функция
, такую что функция
F(z)=U(z)+iV(z)
Является аналитической в этом круге. Такая функция V называется гармонически спряженной с U, а функции U(z) и V(z) – сопряженными гармоническими функциями
U(z)=ReF(z)
F(z) разлагается в степенной ряд 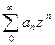 , который равномерно сходиться компактных множествах круга
, который равномерно сходиться компактных множествах круга 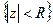
Пусть 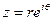 , тогда
, тогда
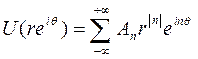 ,
,
где
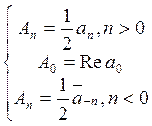
Таким образом, любая функция U(z), гармоническая в круге 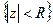 , допускает представление в виде ряда
, допускает представление в виде ряда
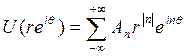
Равномерно сходящегося на компактных подмножествах круга 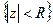 .
.
Дата добавления: 2015-08-14; просмотров: 566;
