Формула Пуассона

Формулу, которую мы вывели в предыдущем пункте, можно записать в замкнутом виде.

Если R > 1, то мы легко находим, что при r < 1

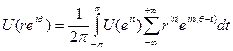
Суммируя две геометрические прогрессии, получаем

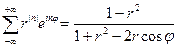при

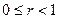
Таким образом, мы приходим к представлению Пуассона: если U(z) — гармоническая функция в {|z| <.R}, где R>1, то при 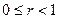имеет место формула

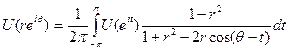
Эта формула является фундаментальной для всей теории. Мы сейчас увидим, что она справедлива при намного более общих условиях, чем указанное выше. Функция

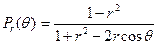
Называется ядром Пуассона для круга {|z|<1}.