Свойства суммируемости гармонических функций, заданных формулой Пуассона

Сначала получим некоторые грубые результаты, достаточные для многих рассмотрений.

Ядро Пуассона

обладает следующими свойствами:

а) Р_r(φ)>0, r< 1;

b)Р_r(φ+2π)= Р_r(φ)

с) 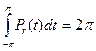для любого r<1.

Свойства а) и b) очевидны, а с) следует из разложения в ряд для Pr(φ).

Если 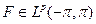то удобно считать, что функция F периодически продолжена на всё множество R: F(t+2π)=F(t). Отныне будем это предполагать.

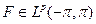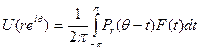Теорема. Если p≥l, , a , то функция U(z) — гармоническая в круге {|z|<1}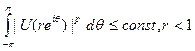

Доказательство.

Пусть 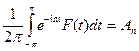. Тогда для 0 ≤r < 1 имеем

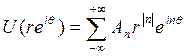
Непосредственно проверяется, что функция U(z) гармонична в {|r|< 1}, так как ряд сходится равномерно во внутренности круга. (Если функция F—вещественная, то ряд, очевидно, является вещественной частью аналитической функции, которая легко выписывается.)

Для данного r < 1 в силу свойства b) и 2π-периодичности функции F мы можем, кроме того, записать

.

Возьмём теперь 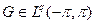,||G||_q=1, так что (для любого фиксированного r; функция G, конечно, будет зависеть от r)

.

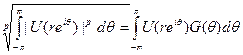По теореме Фубини интеграл справа равен

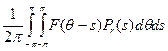
что по модулю не превосходит

(в силу выбора G и свойства с)).

Наконец,

что и требовалось доказать

Теорема. Пусть μ — конечная вещественная мера на [-π,π]. Тогда функция

гармонична в {|r|< 1} и

.

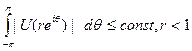Доказательство.

Гармоничность устанавливается так же, как и выше. Пусть дано r, и пусть функция 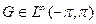, 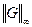= 1, такова, что

-п

Интеграл в правой части по теореме Фубини равен

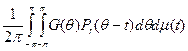
и в силу а)—с) по модулю не превосходит

Вот и всё.