Вычисление области и радиуса сходимости степенного ряда.
Для нахождения радиуса сходимости. как уже отмечалось, обычно используют признаки Коши или Даламбера).
Пример 2. 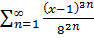
Решение. Будем исследовать ряд на абсолютную сходимость, используя критерий Коши.
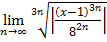 =
=  Для сходимости потребуем:
Для сходимости потребуем: 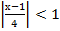 . Тогда распиcав модуль, получим: -3
. Тогда распиcав модуль, получим: -3 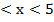 . Значит область сходимости ряда: (-3; 5), радиус сходимости равен половине длины интервала, т.е.R=
. Значит область сходимости ряда: (-3; 5), радиус сходимости равен половине длины интервала, т.е.R= 
Пример 3. Решим этот же пример, используя признак Даламбера.
Составим выражение предела отношений функций 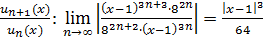
По признаку Даламбера ограничим значение предела единицей: 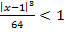 или
или 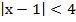 , т.е.
, т.е.
Ряд сходится в средине интервала (-3; 5).
Для определения сходимости на концах интервала следует подставить точки х=. – 3 и х=5 в исходный ряд и поверить сходимость числовых рядов:
1) Так. Пусть х=-3. Тогда имеем знакочередующийся ряд 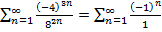 - это есть расходящийся ряд, так как у него нет конечной суммы.
- это есть расходящийся ряд, так как у него нет конечной суммы.
2) х=5. Имеем ряд 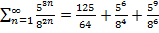 …Это ряд является расходящимися, так как с некоторого момент члены ряда будут представлять дроби, значения числителя которых больше значения знаменателя. Таким образом, окончательный ответ: х
…Это ряд является расходящимися, так как с некоторого момент члены ряда будут представлять дроби, значения числителя которых больше значения знаменателя. Таким образом, окончательный ответ: х 
Дата добавления: 2015-08-11; просмотров: 1053;
