Сходимость степенного ряда.

Одной из особенностей степенных рядов является то, что их сходимость зависит от значения х. Так, например, для ряда 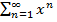при значениях х=1 или х 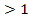ряды являются расходящимся. В тоже время при х 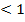ряд представляет убывающую геометрическую прогрессию и кончную сумму при х 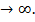Поэтому для степенных рядов характерной задачей является определение интервала сходимости, т.е. найти множество значений «икс», при котором степенной ряд будет сходиться.

Для любого степенного ряда возможны три случая:

1) Степенной ряд сходится абсолютно на некотором интервале 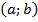. Иными словами, если мы выбираем любое значение «икс» из интервала 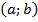и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал 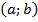и называется интервалом сходимости степенного ряда.

Радиус сходимости, если совсем просто, это половина длины интервала сходимости: R=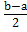
2) Степенной ряд сходится абсолютно при любом значении x. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 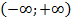. Радиус сходимости: .

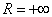2) Степенной ряд сходится в единственной точке. Если ряд имеет вид 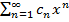, то он будет сходиться в единственной точке

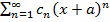3) x=0. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: x=0. Если ряд имеет вид , то он будет сходиться в единственной точке x=a, если ряд имеет вид , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: R=0.