Исследование степенного ряда на cходимость

Задание часто формулируют примерно так : Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.

Алгоритм решения довольно прост.

На первом этапе находим интервал сходимости ряда. Почти всегда необходимо использовать признак Даламбера и находить предел 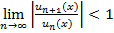. Технология применения исходит из признака Даламбера точно такая же, как и для числовых рядов. Значения этого придела модуля ограничиваем единицей потому, что по признаку Даламбера при таком условии числовые ряды сходятся. Либо используется признак Коши 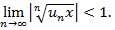Единственное отличие от числового ряда – вычисление происходят под знаком модуля.

Пример 1. Найти область сходимости ряда: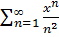

Решение: Составим предельное отношение следующего 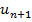члена ряда к предыдущему 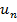и вычислим этот предел:

q= 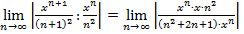= после сокращения и перехода к предельному значению переменной n получим: q= 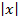, ограничиваем значение этого предела согласно услови Даламбера единицей, т.е.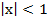

Таким образом, область сходимости нашего ряда есть -1< x < 1.

Отметим другие случаи значений предельных отношений Даламбера.

1. Так, если в пределе получается ноль, то алгоритм решения заканчивает свою работу, и мы даём окончательный ответ задания: «Область сходимости степенного ряда: 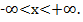То есть, степенной ряд сходится при любом значении «икс».

2. Если в пределе получается бесконечность, то алгоритм решения также заканчивает свою работу, и мы даём окончательный ответ задания: «Ряд сходится при х=0» (или при х=а либо х= -а»).

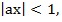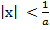3. Если в пределе получается не ноль и не бесконечность, то у нас самый распространенный на практике случае – ряд сходится на некотором интервале т.е. , или - ,

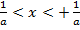где а – это оставшееся значения отношение предела.