Разложение функции в степенной ряд. Ряды Тейлора и Маклорена.

Теорема. Если функция f(x) n раз дифференцируема в некоторой точке 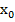, то её можно разложить в окрестности этой точки в степенной ряд 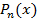(многочлен n- ой степени) вида:

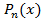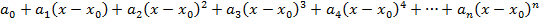= (1)

при условии, что значения функции f(x) и многочлена 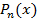и их производные всех порядков совпадают.

Тогда функцию f(x) можно представить как разложение по степеням (х- в виде ряда:

f(x)=f( 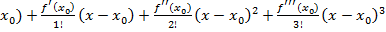+…+ 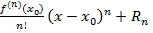, (2)

где коэффициенты выражены через значения производных в точке 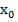и порядковые факториалы,

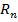- остаток разложения.

Формула (2) называется формулой Тейлора.