Доказательство. Пусть имеется функция f(x)

Пусть имеется функция f(x) . Необходимо представить функцию f(x) многочленом 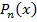вида (1), которые удовлетворяют условию теоремы, т.е. имеют производные n- го порядка и их значения совпадают в точке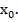

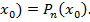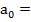Так, предположим, что х= . Получим f( Тогда из уравнения (1) следует, что Значит f(

Теперь дифференцируем f(x) и .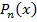

(3)

при х= 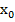получим 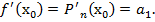таким образом, имеем 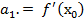(4)

Далее берём производные второго порядка:

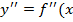); из равенства (3) 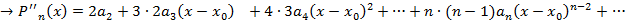(5)

Полагаях = , получим 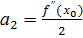(6)

Итак, продолжая дифференцировать последовательно третий раз, четвёртый и т.д., получим: 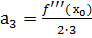, … (7)

Теперь в знаменателях значений коэффициентов (7) произведение чисел заменим факториалами и запишем выражение функции f(x):

f(x)= f( 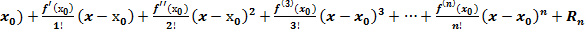(8)

Уравнение (8) называется формулой Тейлора,

где 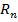-остаточный член формулы Тейлора в форме Лагранжа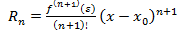

Если разложение функции осуществлять в окрестности точки х=0, то полученный ряд будет представлен более простой и удобной для работы уравнением и называется формулой Маклорена или рядом Маклорена:

f(x)= f( (8)