Доказательство. Пусть подпоследовательность последовательности , где

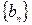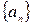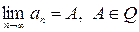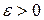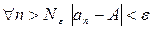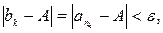Пусть подпоследовательность последовательности , где . Возьмем произвольное рациональное число , тогда в силу сходимости найдется такое , что . Пусть k – произвольное натуральное число, большее . Тогда т.к. 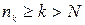. Следовательно, последовательность 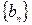сходится к A.

что и требовалось доказать.

Свойство 2 ф.п.р.ч. Любая подпоследовательность фундаментальной последовательности рациональных чисел является фундаментальной последовательностью рациональных чисел.