Доказательство. Первоначально покажем, что алгебра не является ассоциативной.

Первоначально покажем, что алгебра 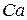не является ассоциативной.

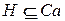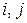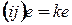
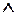
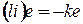
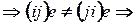
. Рассмотрим кватернионы . 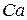не является ассоциативной.

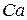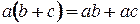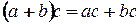Легко самостоятельно проверить, что в алгебре справедливы дистрибутивные законы: и ; умножение удовлетворяет следующему условию: 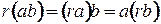для любых 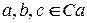и 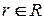; 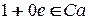- нейтральный элемент по умножению.

Определим в алгебре 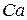для элемента 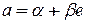сопряженный элемент 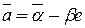, где 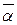- сопряженный к 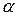в теле кватернионов. В 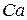справедливы следующие свойства:

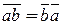для любых .

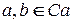Нормой элемента 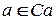договоримся называть . Причем

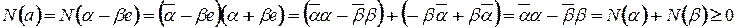
В 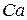справедливы следующие свойства:

1. 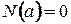т.т.т., к. ;

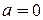2. ;

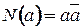3. ;

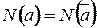4. .

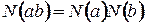для любых .

Замечание.Из свойств 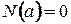т.т.т., к. 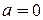и 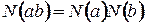следует, что если 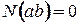, то либо 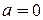, либо .

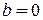Согласно вышеприведенному замечанию, в алгебре 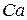отсутствуют делители нуля.

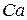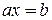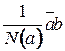Убедимся, что алгебра с делением. Рассмотрим уравнение , где . Элемент является решением данного уравнения. Проверим это.

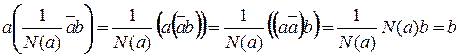. Аналогично устанавливается, что элемент 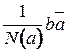является решением данного уравнения 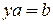, где .

что и требовалось доказать.

Определение.Алгебра 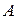над полем 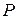называется альтернативной, если выполняется следующие аксиомы:

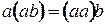
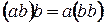
для любых .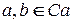

Теорема.Алгебра 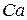над полем 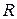является альтернативной.

Замечание. Алгебра 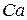над полем 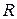является альтернативной, но не ассоциативной. В классе всех альтернативных алгебр лежат и ассоциативные.