Доказательство. Покажем, что - линейное пространство над полем .
Покажем, что 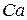 - линейное пространство над полем
- линейное пространство над полем 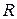 .
.
Сложение в 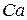 коммутативно и ассоциативно в силу коммутативности и ассоциативности сложения в
коммутативно и ассоциативно в силу коммутативности и ассоциативности сложения в 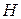 .
.
Нейтральный элемент по сложению в 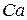 имеет вид:
имеет вид: 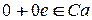 .
.
Противоположным к 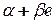 является элемент
является элемент 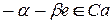 .
.
Таким образом 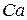 - аддитивная Абелева группа, в которой для
- аддитивная Абелева группа, в которой для 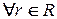 и
и 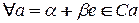 однозначно определено умножение на скаляр
однозначно определено умножение на скаляр  , удовлетворяющее следующим аксиомам:
, удовлетворяющее следующим аксиомам:
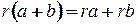
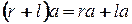

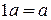
для любых  и
и 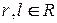 .
.
Согласно определению, 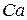 - линейное пространство над полем
- линейное пространство над полем 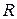 .
.
По теореме о последовательном расширении полей, имеем
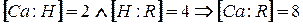 .
.
что и требовалось доказать.
Определим в 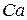 умножение по следующему правилу:
умножение по следующему правилу:
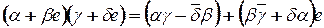 , где
, где 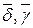 - кватернионы, сопряженные к
- кватернионы, сопряженные к 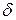 ,
, 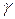 .
.
Теорема. 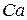 -восьмерная алгебра с делением над полем
-восьмерная алгебра с делением над полем 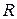 .
.
Дата добавления: 2015-08-21; просмотров: 707;
