Абсолютная и относительная сходимость.

Определение. Числовой ряд (1) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин членов ряда (1), т.е. ряд (2)

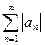(2)

Терема.Всякий абсолютно сходящийся ряд сходится.

Доказательство. Пусть ряд (1) сходится абсолютно. Это будет означать, что для него выполнен критерий Коши сходимости ряда, т.е. для 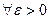существует номер 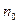, такой, что для всех 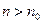выполнялось неравенство

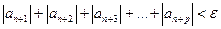
для всех натуральных 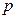. Используем свойства абсолютной величины числа, получаем

.

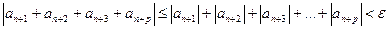Приходим к выводу, что для знакопеременного ряда (1) выполнен критерий Коши, следовательно, он сходится.

Определение.Если ряд (1) сходится, но не абсолютно, он называется условно сходящимся рядом.