Тема2. Функциональные ряды.

Функциональные ряды. Основные понятия.

Пусть 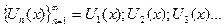-последовательность функций, заданных на некотором множестве Х.

Определение. Выражение вида 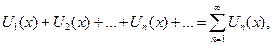(1),

в котором члены последовательности 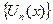соединены знаками плюс, называется функциональным рядом, определенным на множестве Х.

Функции - члены этого функционального ряда.

При фиксированном 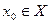всякому функциональному ряду 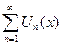соответствует числовой ряд 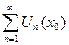, членами которого являются значения 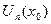функций 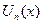в точке .

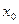Определение. Функциональный ряд (1.1) называют сходящимся в точке 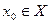, если сходится числовой ряд .

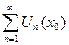Точка 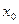называется точкой сходимости функционального ряда (1.1) . Множество всех точек сходимости функционального ряда называется его областью сходимости.

Такую сходимость функционального ряда называют поточечной.

Определение. Конечная сумма 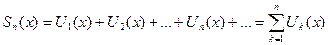называется n-ной частичной суммой ряда(1.1).

Определение. Функция 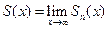, определенная в области D называется суммой ряда (1.1).

Определение. Для всякого 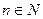функциональный ряд 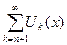, 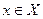называют n-ным остатком функционального ряда (1.1).

Можно записать критерий Коши сходимости функционального ряда.

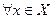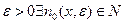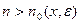Функциональный ряд (1.1) сходится на множестве Х тогда и только тогда, когда для и (зависящее от х и ), такое, что для всех и

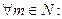
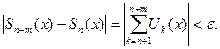
Определение. Функциональный ряд (1.1) называется абсолютно сходящимся на множестве 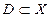, если в любой точке k этого множества сходится ряд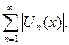

Замечание. Для определения абсолютной сходимости функционального ряда используют признаки Коши и Даламбера.

Примеры.

Найти область сходимости:

1. 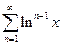, Область определения: .

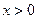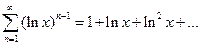-это геометрическая прогрессия,у которой

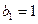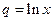
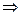, ряд сходится при ,

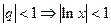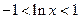
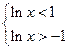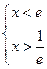; ; т.е. при 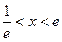- ряд сходится.

Легко найти и сумму этого ряда: .

2. 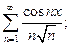Область определения: .

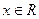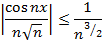
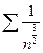- сходится 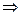по признаку сравнения исходный ряд сходится абсолютно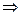 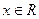область сходимости исследуемого ряда.

3. 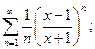Область определения : ,

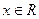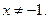
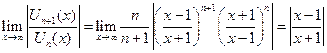; значит ряд сходится при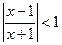

Решим неравенство:

;

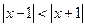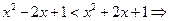
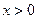- ряд абсолютно сходится;

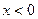-расходится;

при :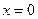

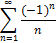
Ряд условно сходится по признаку Лейбница .