Теорема
Для последовательности функции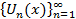 
и функции U(x), определённых на множестве 
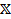, Справедливо следующее утверждение:
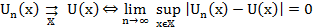
Справка:
Число называется верхней гранью множества Х, если:
1) 
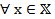уд. неравенству 
2) Для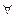 
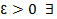
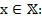
х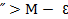 
(или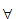 
M’<M 
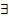x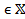 
: x>M’)
Доказательство:
а) Пусть {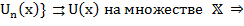 
по определению равн. сходимости:
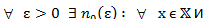
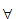n>n0(ε) 
(*).
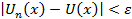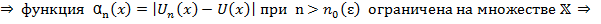
Поэтому для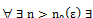 
конечная точная верхняя грань:
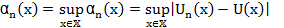
Используя свойство точной верхней грани и определение (*) имеем:
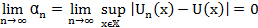
б) Пусть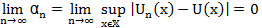 
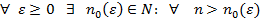
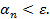
Согласно свойству точной верхней грани, для всех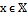 
верно неравенство:
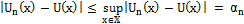
т.е. 
Что по определению означает, что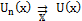 
.
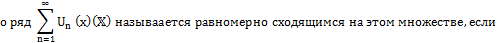
последовательность его частичных сумм равномерно сходится на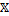 
.
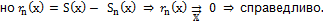
Следствие.
Для равномерной сходимости функционального ряда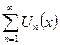 
, необходимо и достаточно, чтобы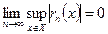 
Пример:
Выяснить, является ли функциональный ряд равномерно сходящимся:
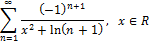
По признаку Лейбница этот ряд сходится в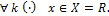 
Оценим остаток ряда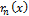 
:
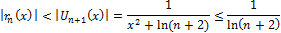
В силу свойства точной верхней грани.
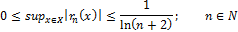
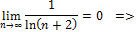
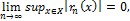т.е.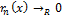 
Дата добавления: 2015-08-11; просмотров: 640;