Доказательство. Ограничимся рассмотрением случая, когда

Ограничимся рассмотрением случая, когда

Обозначим 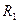– радиус сходимости почленно продифференцированного ряда.

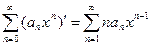
Тогда .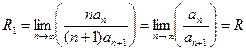

Аналогично:

Пусть 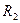– радиус сходимости ряда, полученного почленным интегрированием:

= .

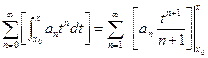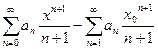Числовой ряд 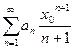сходится абсолютно по признаку сравнения, в силу неравенства

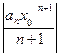
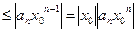
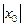
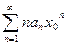-сходится, т.к.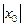 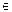(-R;R).

.