Доказательство. Пусть x – произвольная точка интервала сходимости

Пусть x – произвольная точка интервала сходимости. Всегда существует такое число q>0, что |x|<q<R.

По теореме Абеля степенной ряд сходится равномерно на отрезке [-q;q] 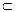(-R;R).

Тогда, согласно теореме (о непрерывности суммы равномерно сходящегося функционального ряда), S(x) непрерывна на отрезке [-q;q], а, следовательно, и в точке x.

В силу произвольности выбора точки x 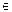(-R;R) получаем непрерывность функции на (-R;R).