Теорема (признак Вейерштрасса).

Если члены функционального ряда 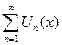удовлетворяют неравенствам:

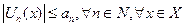(5) и числовой ряд 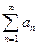, 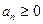-сходится, то функциональный ряд сходится равномерно в области Х.

Доказательство:

Так как числовой ряд сходится, то его остаток стремится к нулю 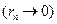, то есть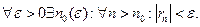

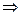
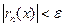
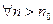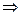и по определению равномерной сходимости ряд 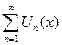-равномерно сходится в области Х.

Числовой ряд 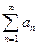, члены которого удовлетворяют неравенству (2.5), называется мажорантным рядом или мажорантой для функционального ряда (1.1).

Функциональный ряд называется мажорируемым на множестве Х.

Замечание:

Признак Вейерштрасса является достаточным для абсолютной сходимости ряд.