Перестановка членов в сходящихся рядах.

Теорема (о перестановке членов ряда).

Если ряд

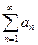(3)

с положительными членами сходится, то после произвольной перестановки членов ряда, полученный ряд будет также сходиться, причем к той же сумме.

Доказательство. Пусть S – это сумма сходящегося ряда (1), т.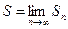е. , где 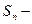частичные суммы ряда (1). Переставим произвольным образом члены ряда (1), получим ряд

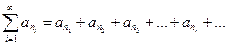(4)

Обозначим 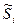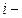ю частичную сумму ряда (4).

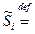
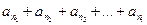. (5)

Вычислим наибольший номер из 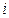членов ряда (4), входящих в частичную сумму (5). 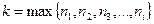. И рассмотрим 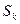- частичную сумму ряда (3) с номером 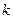. Очевидно, что все члены ряда из частичной суммы (5) будут содержаться в .

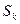Тогда 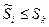. В силу того, что члены ряда (3) положительны, то любая его частичная сумма, в том числе и 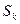, не превосходит суммы ряда, таким образом, приходим к неравенству

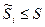. (6)

Мы получили, что неубывающая последовательность 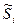ограничена сверху - значит, она имеет предел. Пусть

.

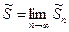Из неравенства (6) после предельного перехода будет следовать, что 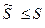. Получается, что при перестановке членов ряда сумма не увеличивается, но она не может и уменьшиться, т.к. при обратной перестановке сумма бы увеличивалась, что противоречит полученному результату. Тогда

.

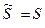Теорема доказана.