Свойства равномерно сходящихся рядов
Замечание: Если два функциональных ряда 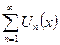 и
и 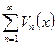 сходятся на множестве X равномерно, то всякая их линейная комбинация ,
сходятся на множестве X равномерно, то всякая их линейная комбинация , 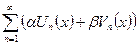 где a,bÎR
где a,bÎR  так же является равномерно сходящимся рядом на множестве X.
так же является равномерно сходящимся рядом на множестве X.
Теорема Если функции 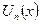 непрерывны в точке
непрерывны в точке 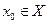 ряд
ряд 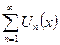 - равномерно сходящийся на множестве X, то его сумма
- равномерно сходящийся на множестве X, то его сумма 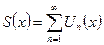 так же непрерывна в точке
так же непрерывна в точке 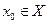 .
.
Доказательство.
Напомним определение: Функция непрерывна в точке 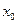 , если она определена в этой точке, существует предел функции в этой точке и равен значению функции в точке, т.е.
, если она определена в этой точке, существует предел функции в этой точке и равен значению функции в точке, т.е. 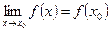 или
или 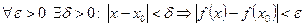
1) Ряд 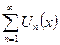 - равномерно сходящийся
- равномерно сходящийся
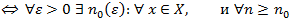
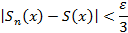
Последнее неравенство выполняется для 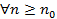 , в том числе и для любого фиксированного
, в том числе и для любого фиксированного 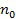 , т.е.
, т.е.
2) Частичная сумма ряда - функция 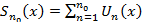 - непрерывна, как сумма конечного числа непрерывных функций она непрерывна и в точке
- непрерывна, как сумма конечного числа непрерывных функций она непрерывна и в точке 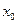 .
.
Оценим разность
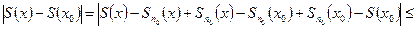
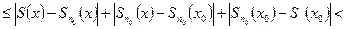

т.е. 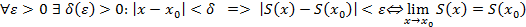 , т.е. функция
, т.е. функция 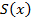 - непрерывна в точке
- непрерывна в точке 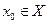
Следствие 1. Если сумма 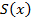 функционального ряда с непрерывными членами разрывна в области
функционального ряда с непрерывными членами разрывна в области 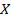 , то этот ряд в области
, то этот ряд в области 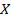 сходится неравномерно.
сходится неравномерно.
Следствие 2 В равномерно сходящемся ряде возможен почленный переход к пределу, т.е.
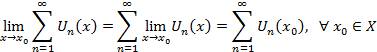
Т.к. 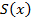 - непрерывная функция, то
- непрерывная функция, то 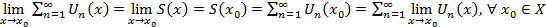
Пример
Исследовать характер сходимости ряда 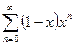 на сегменте 0£x£1
на сегменте 0£x£1
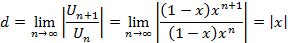
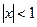
при х=0 0+0+0+… ряд сходится;
при х=1 0+0+0+… ряд сходится;
Частичные суммы ряда
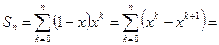
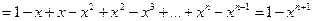 .
.
Тогда предел частичных сумм
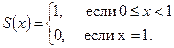
Остаток ряда 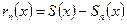 .
.
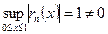
Следовательно, данный ряд сходится неравномерно на исследуемом отрезке.
Примечание. Если функциональный ряд непрерывных на сегменте функций сходится на этом сегменте к разрывной функции, то ряд сходится неравномерно.
Замечание (следствие теоремы о непрерывности суммы неравномерно сходящегося ряда)
Если сумма S(x) функционального ряда с непрерывными членами разрывна в области X, то этот ряд в области X сходится неравномерно.
Следствие : В равномерно сходящемся ряде возможен почленный переход к пределу. 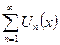 – сходится равномерно тогда S(x) - непрерывная функция.
– сходится равномерно тогда S(x) - непрерывная функция.
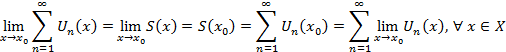
т.е.
Теорема (о почленном интегрировании функционального ряда).
Если функциональный ряд 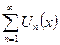 с непрерывными членами сходится кфункции S(x) равномерно на [a,b], то его можно почленно интегрировать на любом отрезке
с непрерывными членами сходится кфункции S(x) равномерно на [a,b], то его можно почленно интегрировать на любом отрезке 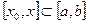 и справедливо равенство:
и справедливо равенство:
 (1)
(1)
и ряд 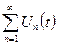 сходится равномерно на отрезке [a;b].
сходится равномерно на отрезке [a;b].
Доказательство:
1.Согласно теореме о непрерывности равномерно сходящегося функционального ряда функция 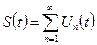 непрерывна на отрезке [a;b], следовательно, она интегрируема на любом отрезке
непрерывна на отрезке [a;b], следовательно, она интегрируема на любом отрезке 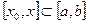 .
.
2. Ряд 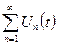 сходится равномерно на отрезке [a;b] это означает, что
сходится равномерно на отрезке [a;b] это означает, что
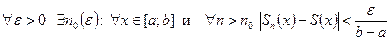
Обозначим:
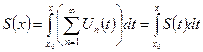
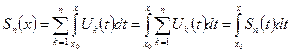
Оценим разность:
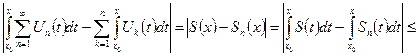
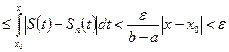
Для 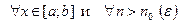 , следовательно, ряд
, следовательно, ряд  сходится на отрезке [a;b] равномерно к функции
сходится на отрезке [a;b] равномерно к функции 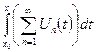 , т.е. справедливо равенство (1).
, т.е. справедливо равенство (1).
Пример:
Исследовать на сходимость ряд 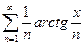 .
.
Рассмотрим ряд:
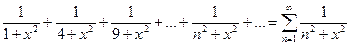
Для любого действительного числа 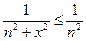 , а ряд
, а ряд 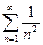 - сходящийся, следовательно, по признаку Вейерштрасса ряд
- сходящийся, следовательно, по признаку Вейерштрасса ряд 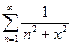 - сходится равномерно на всей числовой оси.
- сходится равномерно на всей числовой оси.
Проинтегрируем его на отрезке [0;x]
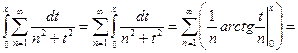
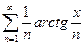
По теореме о почленном интегрировании функциональных рядов он сходится равномерно на всей числовой оси.
Теорема ( о почленном дифференцировании функционального ряда)
Если функциональный ряд 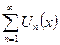 с непрерывно дифференцируемыми на отрезке [a;b] членами сходится к функции S(x), а ряд
с непрерывно дифференцируемыми на отрезке [a;b] членами сходится к функции S(x), а ряд 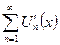 – сходится равномерно на этом отрезке, то исходный ряд
– сходится равномерно на этом отрезке, то исходный ряд 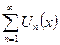 - сходится равномерно на[a;b] , его сумма S(x) – непрерывно дифференцируемая функция и справедливо равенство
- сходится равномерно на[a;b] , его сумма S(x) – непрерывно дифференцируемая функция и справедливо равенство
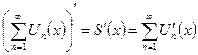 (2)
(2)
Доказательство:
Обозначим через 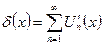 .
.
Проинтегрируем это равенство на 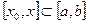
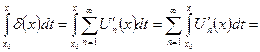
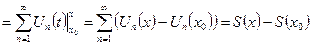
(Левая часть полученного равенства дифференцируема по x , следовательно, и правая часть дифференцируема по x) 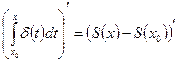 тогда
тогда 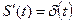 , следовательно, справедливо равенство (2).
, следовательно, справедливо равенство (2).
Равномерная сходимость ряда 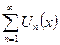 следует из предыдущей теоремы.
следует из предыдущей теоремы.
Пример:
Найти сумму ряда:
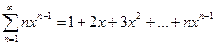
Ряд 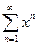 сходится при
сходится при 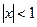 .
. 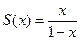 .
.
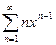 сходится при
сходится при 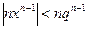 ,
, 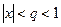 т.е. сходится равномерно по признаку Вейерштрасса,
т.е. сходится равномерно по признаку Вейерштрасса, 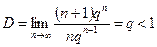 – сходится,
– сходится,
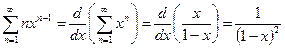
§4 Степенные ряды
Определение: Ряд вида:
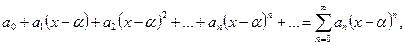 (1)
(1)
где 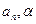 - действительные числа – называется степенным рядом по степеням
- действительные числа – называется степенным рядом по степеням 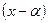 ,
, 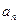 - коэффициенты степенного ряда.
- коэффициенты степенного ряда.
При α=0, получаем ряд
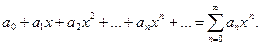 (2)
(2)
В дальнейшем будем рассматривать ряды вида (2) т.к. ряды вида (1) приводится к виду (2) заменой переменной x-a=t.
Для степенных рядов справедлива
Теорема (теорема Абеля).
Если степенной ряд 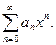 сходится в точке
сходится в точке 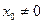 , то он сходится абсолютно в интервале
, то он сходится абсолютно в интервале 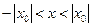 и сходится равномерно на отрезке -q£x£q,
и сходится равномерно на отрезке -q£x£q, 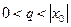 .
.
Доказательство :
1) Т.к. по условию теоремы числовой ряд 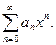 - сходится, тогда
- сходится, тогда 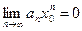 , всякая сходящаяся последовательность – ограничена, следовательно,
, всякая сходящаяся последовательность – ограничена, следовательно, 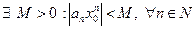 .
.
Пусть 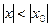 , тогда рассмотрим
, тогда рассмотрим 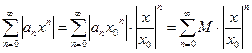 .
.
Члены ряда 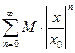 - образуют геометрическую прогрессию со знаменателем
- образуют геометрическую прогрессию со знаменателем 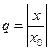 . Что бы этот ряд сходился необходимо и достаточно
. Что бы этот ряд сходился необходимо и достаточно 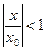 ,
, 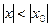 , т.е. ряд (2) сходится абсолютно при
, т.е. ряд (2) сходится абсолютно при 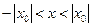 .
.
2). Если 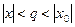 , то
, то 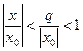 . Ряд (2) мажорируется сходящимся числовым рядом
. Ряд (2) мажорируется сходящимся числовым рядом 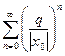 , следовательно, по признаку Вейерштрасса он сходится равномерно на отрезке [-q;q].
, следовательно, по признаку Вейерштрасса он сходится равномерно на отрезке [-q;q].
Следствие :
Если в точке 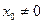 , степенной ряд
, степенной ряд 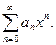 расходится, то он расходится во всех точках х, таких что
расходится, то он расходится во всех точках х, таких что 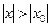
Из теоремы Абеля и следствия вытекает, что если степенной ряд 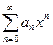 , сходящийся хотя бы в одной точке
, сходящийся хотя бы в одной точке 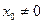 , то всегда существует число R>0 и степенной ряд сходится абсолютно для всех xÎ(-R;R) и расходится во всех
, то всегда существует число R>0 и степенной ряд сходится абсолютно для всех xÎ(-R;R) и расходится во всех 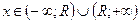 .
.
При x= ±R ряд может, как сходится, так и расходится.
Неотрицательное число R называется радиусом сходимости ряда. Интервал (-R;R)называется интервалом сходимости. (радиус сходимости R– половина интервала сходимости).
Для нахождения радиуса сходимости степенного ряда используют признаки Даламбера и Коши и формулы для радиуса сходимости, получающиеся из этих признаков.
1. 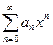
Пусть 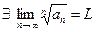 , тогда
, тогда 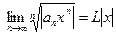 , при
, при 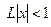 – ряд сходится абсолютно; при
– ряд сходится абсолютно; при 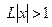 - расходится, следовательно
- расходится, следовательно 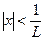 ;
;
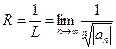 (3)
(3)
2.Аналогично из признака Даламбера
Пусть 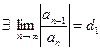 , тогда
, тогда 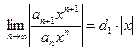 . Если
. Если 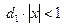 , то
, то 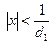 . Тогда
. Тогда
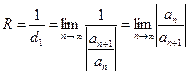
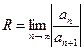 . (4)
. (4)
Пример1 :
Найти радиус сходимости ряда 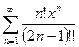 :
:
Имеем 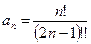 ,
, 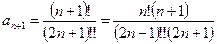 . Найдем предел
. Найдем предел
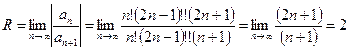 .
.
Пример 2Найти область сходимости ряда 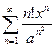 (a>1)
(a>1)
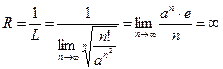
Следовательно, ряд сходится на всей числовой оси.
Дата добавления: 2015-08-11; просмотров: 1718;
