Ряды Тейлора
Пусть функция f(x) имеет в окрестности точки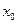 
производные любого порядка. Поставим ей в соответствие степенной ряд:
~ 
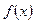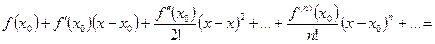
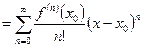(1)
Этот ряд называется рядом Тейлора функцииf(x) в точке .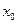
Если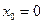 
, то ряд Тейлора имеет вид:
~ 
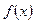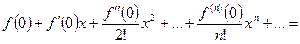
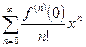(2)
и называется рядом Маклорена.
Радиус сходимости степенного ряда (1) может быть как равным 0, так и отличным от 0, причём в последнем случае сумма S(x) ряда Тейлора может не совпадать с f(x).
Необходимо выяснить вопрос о том, когда в соотношении (1) можно поставить знак равенства, то есть когда ряд Тейлора сходится к функции, для которой он составлен.
Если S(x)= f(x) на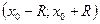 
, то говорят, что функцияf(x) разложима в ряд Тейлора в окрестности точки .
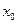Обратимся к следующей теореме.
Теорема 23:
Для того, чтобы бесконечно дифференцируемая в окрестности точки 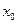функция f(x)разлагалась в ряд Тейлора в окрестности этой точки, необходимо и достаточно, что бы 
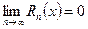для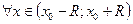 
Частичные суммы ряда (1) представляют собой многочлены Тейлора 
функции f(x)точке 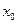. Выпишем последовательность частичных сумм
;
;
;
…………………………………………….
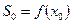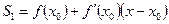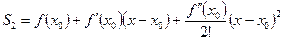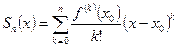
Если ряд сходится к функции f(x)., справедливо равенство
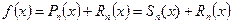
Откуда следует, что
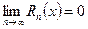
Обратим внимание на то, что в формуле (1) участвует остаточный член ряда Тейлора, а не остаточный член формулы Тейлора. (В общем случае они различны).
Остаток формулы Тейлора представим в одном из следующих видов:
Форма Лагранжа:
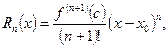
где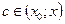 
.
Форма Пеано:
.
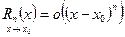На практике часто используется следующий достаточный признак разложимости функции в ряд Тейлора:
Теорема :
Если для 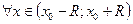все производные функции f(x). ограничены одной и той же константой M, то ряд Тейлора (1) сходится к функции f(x).в интервале 
.
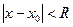Доказательство:
Возьмём остаточный член формулы Тейлора в форме Лагранжа:
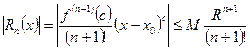
При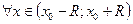
Числовой ряд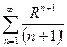 
– сходится так как
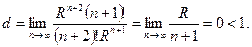
Следовательно, на основании необходимого признака сходимости ряда:
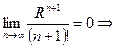
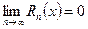при .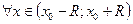
Определение Действительную функцию f(x). действительного переменного называют аналитической в точке 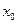, если она определена в некоторой окрестности этой точки, и её можно представить некоторым сходящимся степенным рядом:
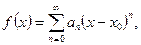
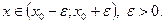
Такое представление аналитической функции называют её разложением в степенной ряд в окрестности точки .
Следующая теорема показывает, что разложение аналитической функции в степенной ряд единственно и этим рядом является её ряд Тейлора.
Теорема. Если в некоторой окрестности точки х для функции f(x). справедливо разложение
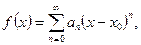
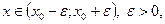
то функция f(x). бесконечно дифференцируема в этой окрестности и
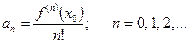
Доказательство:
Пусть 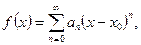- некоторое разложение функции f(x). в степенной ряд в окрестности 
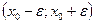точки 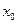и R радиус сходимости этого ряда. Тогда 
. Согласно свойствам степенного ряда этот ряд можно почленно дифференцировать в интервале сходимости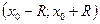 
любое число раз. Поэтому для 
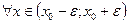имеем
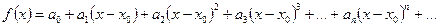
То есть
………………………………………………………………..
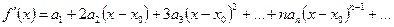
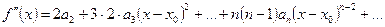
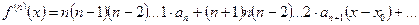
Полагая в этих равенствах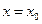 
получаем:
……………………..
…………………………..
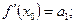
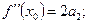
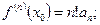
Т.е.
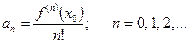
Таким образом, аналитическую в точке 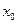функцию можно определить как функцию, которая в некоторой окрестности точки 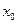является суммой своего ряда Тейлора.
Дата добавления: 2015-08-11; просмотров: 899;