Разложение некоторых элементарных функций в ряды Тейлора, Маклорена
Для приложений важно уметь данную функцию  разлагать в степенной ряд, т.е. функцию
разлагать в степенной ряд, т.е. функцию  представлять в виде суммы степенного ряда.
представлять в виде суммы степенного ряда.
Для любой функции 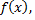 определенной в окрестности точки
определенной в окрестности точки  и имеющей в ней производные до
и имеющей в ней производные до 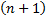 -го порядка включительно, справедлива формула Тейлора
-го порядка включительно, справедлива формула Тейлора
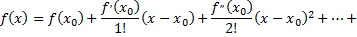
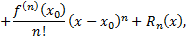
где
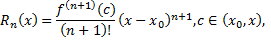
остаточный член в форме Лагранжа. Число 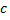 можно записать в виде
можно записать в виде
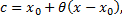
где 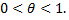
Если функция  имеет производные любых порядков в окрестности точки
имеет производные любых порядков в окрестности точки  и остаточный член
и остаточный член 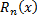 стремится к нулю при
стремится к нулю при 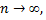 то из формулы Тейлора получается разложение функции
то из формулы Тейлора получается разложение функции  по степеням
по степеням 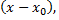 называемое рядом Тейлора
называемое рядом Тейлора

Если в ряде Тейлора положить  то получим разложение функции по степеням
то получим разложение функции по степеням  в ряд Маклорена
в ряд Маклорена
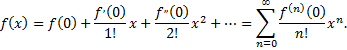
Для того, чтобы ряд Тейлора функции  сходился к
сходился к  в точке
в точке  необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремится к нулю при
необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремится к нулю при 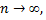 т.е. чтобы
т.е. чтобы
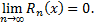
Если модули всех производных функций  ограничены в окрестности точки
ограничены в окрестности точки  одним и тем же числом
одним и тем же числом  то для любого
то для любого  из этой окрестности ряд Тейлора функции
из этой окрестности ряд Тейлора функции  сходится к функции
сходится к функции 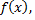 т.е. имеет место разложение
т.е. имеет место разложение

Разложение некоторых элементарных функций в ряд Тейлора (Маклорена).
Для разложения функции  в ряд Маклорена нужно:
в ряд Маклорена нужно:
1) найти производные 
2) вычислить значения производных в точке 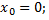
3) написать ряд
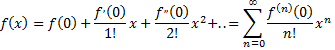
для заданной функции и найти его интервал сходимости;
4) найти интервал 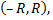 в котором остаточный член ряда Маклорена
в котором остаточный член ряда Маклорена 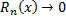 при
при  Если такой интервал существует, то в нем функция
Если такой интервал существует, то в нем функция  и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.
Разложение в ряд Маклорена некоторых элементарных функций:

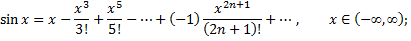
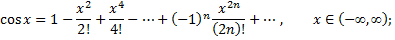
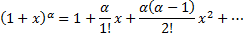
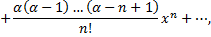
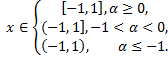
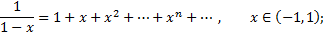

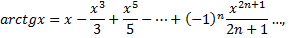
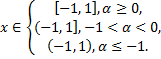
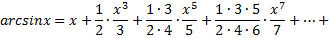

Рассмотрим пример. Разложить в ряд функцию
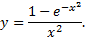
Так как по

то, заменяя  на
на 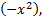 получим
получим
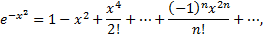
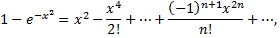
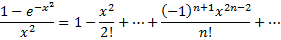
Область сходимости ряда 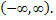
Рассмотрим пример. Разлить в ряд функцию
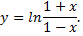
В разложении

заменим  на
на 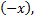 получим
получим
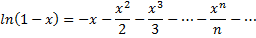
Теперь
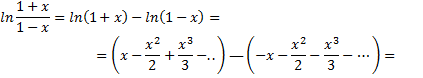
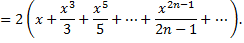
Область сходимости ряда 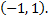
Дата добавления: 2015-08-11; просмотров: 2938;
