Периодические функции
При изучении разнообразных периодических процессов, т.е. процессов, которые через определенный промежуток времени повторяются (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т.д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в тригонометрический ряд.
Функция 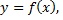 определенная на множестве
определенная на множестве 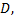 называется периодической с периодом
называется периодической с периодом 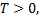 если при каждом
если при каждом 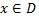 значение
значение 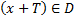 и выполняется равенство
и выполняется равенство 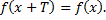
Для построения графика периодической функции периода  достаточно построить его на любом отрезке длины
достаточно построить его на любом отрезке длины  и периодически продолжать его во всю область определения.
и периодически продолжать его во всю область определения.
Основные свойства периодической функции.
1)Алгебраическая сумма периодических функций, имеющих один и тот же период 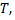 есть периодическая функция с периодом
есть периодическая функция с периодом 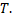
2)Если функция  имеет период
имеет период 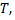 то функция
то функция  имеет период
имеет период 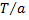
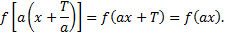
3)Если функция  имеет период
имеет период  и интегрируема на отрезке
и интегрируема на отрезке 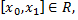 то
то

при любых  и
и 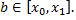
Простейшими периодическими функциями являются тригонометрические функции 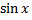 и
и 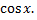 Период этих функций равен
Период этих функций равен 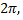 т.е.
т.е. 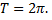
Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией

где  амплитуда колебания,
амплитуда колебания, 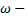 частота,
частота, 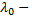 начальная фаза.
начальная фаза.
Функцию такого вида называют простой гармоникой. Основным периодом функции
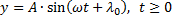
является

т.е. одно полное колебание совершается за промежуток времени
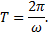
При наложении простых гармоник получается периодическая функция, описывающая сложное периодическое колебание (периодический процесс).
С помощью тригонометрического ряда любую периодическую функцию можно представить в виде ряда, членами которого являются гармоники.
Тригонометрическим рядом называется функциональный ряд вида
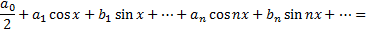
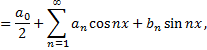
где действительные числа 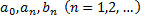 называются коэффициентами ряда.
называются коэффициентами ряда.
Ряд
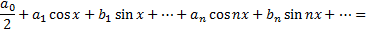

можно записать в виде
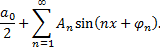
Действительно, положив

получим
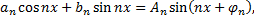
ряд
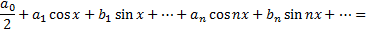

примет вид
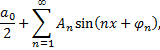
при этом
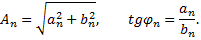
Свободный член ряда записан в виде 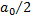 для единообразия получающихся в дальнейшем формул.
для единообразия получающихся в дальнейшем формул.
Приведем формулы, которые понадобятся в дальнейшем.
Считая  и
и  целыми положительными числами, получим
целыми положительными числами, получим
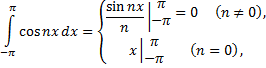
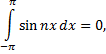
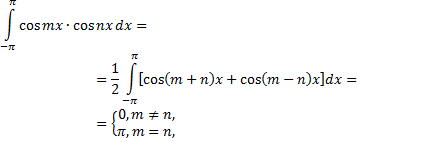
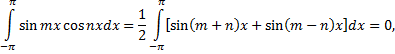
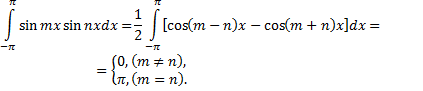
Дата добавления: 2015-08-11; просмотров: 1077;
