Ряды Фурье четных и нечетных периодических функций с произвольным периодом
Если разлагаемая на отрезке 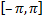 в ряд Фурье функция
в ряд Фурье функция  является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится неполным).
является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится неполным).
Если функция  четная, то ее ряд Фурье имеет вид
четная, то ее ряд Фурье имеет вид
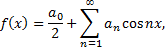
где
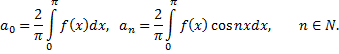
Если функция  нечетная, то ее ряд Фурье имеет вид
нечетная, то ее ряд Фурье имеет вид
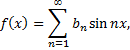
где
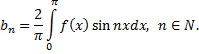
Рассмотрим пример. Разложить в ряд Фурье функцию 
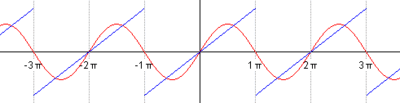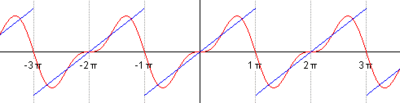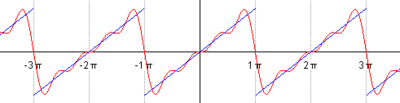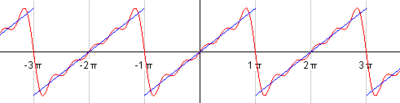
Рис. 67
На рисунке 67 изображен график заданной функции. Условиям Дирихле функция 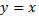 удовлетворяет. Эта функция – нечетная. Следовательно,
удовлетворяет. Эта функция – нечетная. Следовательно, 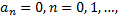 а
а
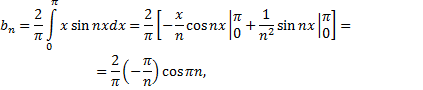
т.е.
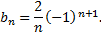
Ряд Фурье содержит только синусы
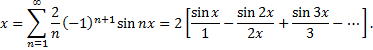
Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от 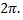
Пусть функция 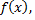 определенная на отрезке
определенная на отрезке 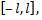 имеет период
имеет период 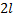
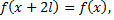
где 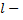 произвольное положительное число, и, функция
произвольное положительное число, и, функция  удовлетворяет на этом отрезке условиям Дирихле.
удовлетворяет на этом отрезке условиям Дирихле.
Сделав подстановку
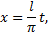
данную функцию  преобразуем в функцию
преобразуем в функцию
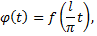
которая определена на отрезке 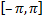 и имеет период
и имеет период 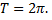
Действительно, если  то
то 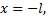 если
если 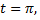 то
то 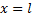 и при
и при 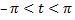 имеем
имеем 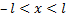

т.е.
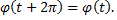
Разложение функции 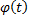 в ряд Фурье на отрезке
в ряд Фурье на отрезке 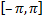 имеет вид
имеет вид
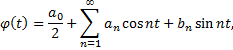
где
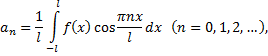
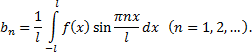
Ряд
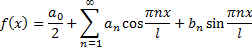
называется рядом Фурье для функции  с периодом
с периодом 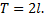
Все теоремы, имеющие место для рядов Фурье  периодических функций, остаются в силе и для рядов Фурье функций, период которых
периодических функций, остаются в силе и для рядов Фурье функций, период которых 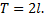 В частности, если
В частности, если  на отрезке
на отрезке 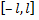 четная, то ее ряд Фурье имеет вид
четная, то ее ряд Фурье имеет вид
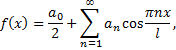
где
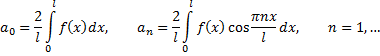
Eсли  на отрезке
на отрезке 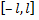 четная, то ее ряд Фурье имеет вид
четная, то ее ряд Фурье имеет вид
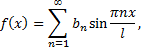
где
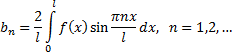
Рассмотрим пример. Разложить функцию 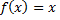 на интервале
на интервале 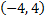 в ряд Фурье.
в ряд Фурье.
Данная функция нечетная, удовлетворяет условиям Дирихле. Согласно формулам
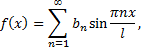
где
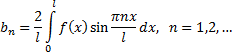
при 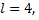 имеем
имеем
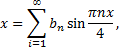
где
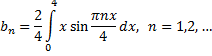
Вычисляем 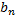

Таким образом,
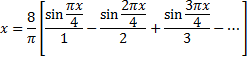
для 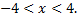
Пусть 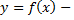 непериодическая функция, заданная на всей числовой оси
непериодическая функция, заданная на всей числовой оси 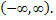
Такая функция не может быть разложена в ряд Фурье, так как сумма ряда Фурье есть функция периодическая и, следовательно, не может быть равна  для всех
для всех 
Однако непериодическая функция  может быть представлена в виде ряда Фурье на любом конечном промежутке
может быть представлена в виде ряда Фурье на любом конечном промежутке 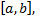 на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка
на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка  и построить функцию
и построить функцию  периода
периода 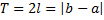 такую, что
такую, что 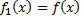 при
при 
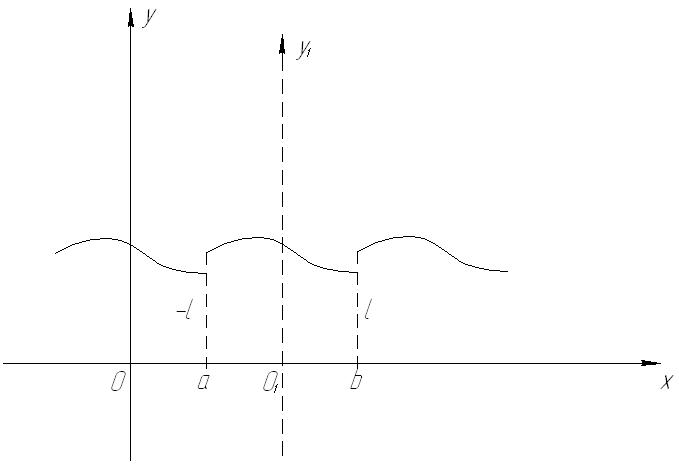
Рис. 68
Непериодическая функция
Разлагаем функцию 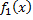 в ряд Фурье. Сумма этого ряда во всех точках отрезка
в ряд Фурье. Сумма этого ряда во всех точках отрезка  (кроме точек разрыва) совпадает с заданной функцией
(кроме точек разрыва) совпадает с заданной функцией 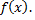 Вне этого промежутка сумма ряда и
Вне этого промежутка сумма ряда и  являются различными функциями.
являются различными функциями.
Пусть теперь непериодическую функцию  требуется разложить в ряд Фурье на отрезке
требуется разложить в ряд Фурье на отрезке 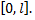 Это частный случай: начало координат перенесено в точку
Это частный случай: начало координат перенесено в точку 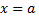 отрезка
отрезка 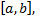 область определения
область определения  будет иметь вид
будет иметь вид  где
где 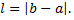
Такую функцию можно произвольным образом доопределить на отрезке 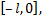 а затем осуществить ее периодическое продолжение с периодом
а затем осуществить ее периодическое продолжение с периодом 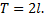 Разложив в ряд Фурье на отрезке
Разложив в ряд Фурье на отрезке 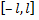 полученную таким образом периодическую функцию
полученную таким образом периодическую функцию 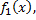 искомый ряд для функции
искомый ряд для функции  при
при 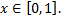
В частности, функцию  можно доопределить на отрезке
можно доопределить на отрезке 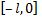 четным образом, т.е. чтобы при
четным образом, т.е. чтобы при 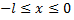 было
было 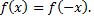 В этом случае функция
В этом случае функция  разлагается в ряд Фурье, который содержит только косинусы.
разлагается в ряд Фурье, который содержит только косинусы.
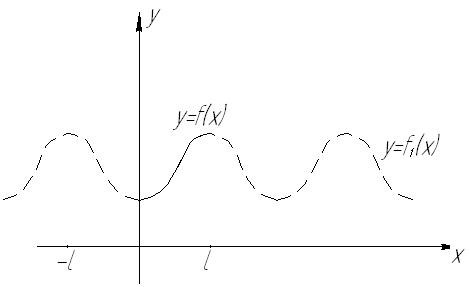
Рис. 69
Непериодическая функция
Если же функцию  продолжить на отрезке
продолжить на отрезке 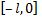 нечетным образом, то она разлагается в ряд Фурье, состоящий только из синусов.
нечетным образом, то она разлагается в ряд Фурье, состоящий только из синусов.
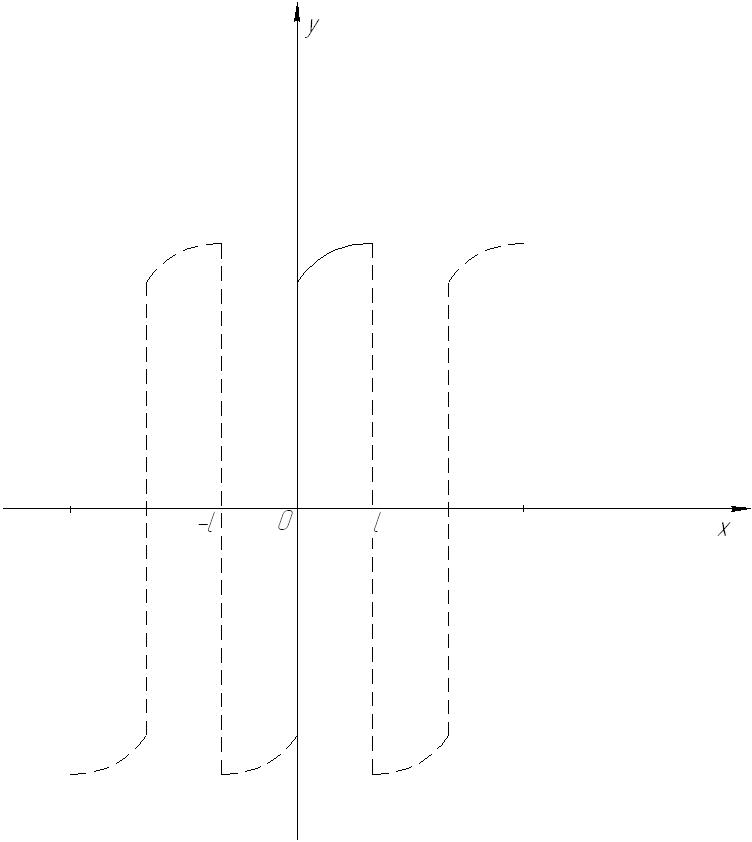
Рис. 70
Ряд косинусов и ряд синусов для функции 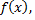 заданной на отрезке
заданной на отрезке  имеют одну и ту же сумму. Если
имеют одну и ту же сумму. Если  точка разрыва функции
точка разрыва функции 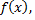 то сумма как одного, так и другого ряда равна одному и тому же числу
то сумма как одного, так и другого ряда равна одному и тому же числу
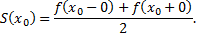
Рассмотрим пример. Разложить в ряд косинусов функцию
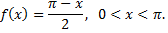
Продолжим функцию  на отрезке
на отрезке 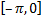 четным образом. Разлагаем в ряд функцию
четным образом. Разлагаем в ряд функцию
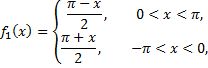
с периодом 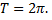 условиям теоремы Дирихле функция
условиям теоремы Дирихле функция  удовлетворяет. Находим
удовлетворяет. Находим
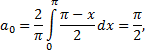
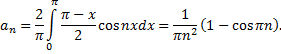
Таким образом,
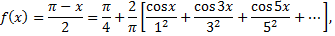
где 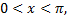 при
при
Контрольные вопросы
1. Дать определение периодической функции и перечислить ее основные свойства.
2. Какой ряд называется тригонометрическим?
3. Записать формулы для нахождения коэффициентов Фурье.
Дата добавления: 2015-08-11; просмотров: 2324;
