Операции над множествами

Рассмотрим операции, которые заданы для двух различных множеств. Множество таких операций относятся к бинарным операциям.

Пусть даны два множества 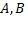и множество , которое является результатом операций над ними.

1)Пересечение множеств состоит из элементов принадлежащих каждому из данных множеств. Обозначается:

Ç .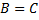

Эту операцию называют еще умножением множеств.

Обозначают пересечение множеств следующим образом

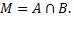
В пересечение входят только те элементы, которые принадлежат каждому из данных множеств, а именно являются общими элементами для всех заданных множеств.

2)Объединение множеств состоит из элементов, принадлежащих хотя бы одному из данных множеств. Эту операцию еще называют сложением множеств. Обозначается объединение множеств

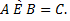
3)Разность множеств состоит их элементов, принадлежащих первому множеству , но не принадлежащих второму множеству 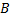. Обозначается: 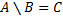. 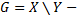вычитание множеств. В разность входят элементы уменьшаемого, без элементов, входящих в вычитаемое множество.

В связи с тем, что результат любой операции является множеством той же предметной области, то такой результат может участвовать в качестве аргумента в последующей операции. Это позволяет строить сложные формулы, описывающие множество через другие множества. Например,

Две формулы и 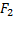называются эквивалентными, если они описывают равные множества. Записывают это в виде равенства .

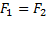Над множествами можно выполнять операции.

Свойства операций:

1) 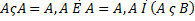– законы поглощения;

2) 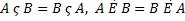– коммутативный (переместительный) закон операции пересечения;

3) 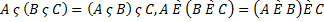— ассоциативный (сочетательный) закон операции пересечения;

4) 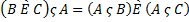– дистрибутивный (распределительный) закон операции пересечения по отношению к объединению;

5) 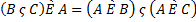– дистрибутивный (распределительный) закон операции объединения по отношению к пересечению.

Декартовым произведением двух множеств называется множество пар элементов, у которых первая компонента принадлежит первому множеству, вторая – второму.

Число элементов декартового произведения, равно произведению мощностей данных множеств

Декартово произведение задается таблицей, координатной плоскостью.

Пусть даны два множества

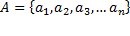и .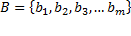

Декартово произведение 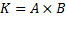есть множество пар вида 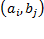, где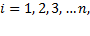

Выбирая из него любое подмножество , получаем соответствие между некоторым подмножеством множества , состоящего из первых компонентов выбранных пар и некоторым подмножеством множества , состоящего из вторых компонентов выбранных пар. 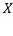– называют областью определения, а – множеством значения соответствия . Причем, возможны случаи, когда 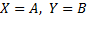одновременно или один из них.

Соответствием между двумя множествами является любое подмножество декартового произведения этих множеств.

Соответствием между двумя множествами называется правило, по которому каждому элементу множества выбирается (устанавливается, определяется) элемент из множества .

Если рассматривать все пары декартового произведения, то пара 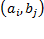задает соответствие между элементами множества 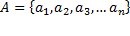и множества 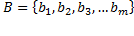с соответствующими областями определения и значения.

Соответствие задается всеми способами, которыми задается декартово произведение двух множеств. Если соответствие задается на координатной плоскости, то область определения соответствия указывается на оси абсцисс, множество значений на оси ординат.

Если во всех парах, задающих соответствие , компоненты поменять местами, то получится соответствие 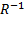, обратное данному соответствию.

Примеры соответствий:

1)график дежурства учащихся на неделю. Область определения – список учащихся. Множество значений – дни недели дежурства;

2)таблица квадратов натуральных чисел. Область определения – натуральные числа. Множество значений – их квадраты;

3)формула 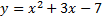задает соответствие между множеством действительных чисел 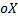– область определения и множеством действительных чисел, являющихся значениями этой формулы – ось .

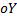Одним из важных понятий математики, есть понятие отображения, которое непосредственно связано с понятием соответствия, описывая его. Понятие отображения часто ассоциируется с понятием функции.

Для задания отображения функции необходимо указать:

1) область определения – множество, которое отображается. Область определения задается изначально и обозначается 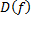. Элементы области определения называют аргументами;

2) область значений – множество, к которому или на которое отображается заданная область, область значений и обозначается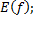

3) правило (закон, соответствие) между .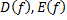

Для задания отображений используются следующие основные способы:

1)аналитический способ – в виде формулы;

2)табличный способ. В первой строчке таблицы записываются элементы (числа) области определения, во второй – элементы множества значений;

3)графический способ – на координатной плоскости;

4)с помощью графов - двух кругов или иных геометрических фигур и стрелок;

5)словесный способ – в виде текста, описывающего закон соответствия.

Отображения делятся на два вида: отображения “в” и “на”.

Пусть задано отображение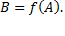

1) Отображение “в” – инъекция. Соответствие, при котором каждому элементу множества соответствует единственный элемент множества , а каждому элементу множества соответствует не более одного прообраза из множества . При этом, мощность множества меньше мощности множества .

2) Отображение “на” – сюръекция. Соответствие, при котором каждому элементу множества соответствует единственный элемент множества , а каждому элементу множества соответствует хотя бы один прообраз из . При этом, мощность множества больше или равна мощности множества .

Особое место занимают взаимно-однозначные отображения (соответствия).

Взаимно-однозначное отображение – биекция. Соответствие, при котором каждому элементу множества соответствует единственный элемент множества и каждому элементу множества соответствует один прообраз из множества . При этом мощность множества равна мощности множества .

Множества будут равномощными (равносильными, эквивалентными), если между ними можно установить взаимно-однозначное соответствие.

Для взаимно-однозначных отображений, обратное отображение также является взаимно-однозначным отображением.

Например, установить взаимно-однозначные соответствия между следующими равномощными множествами:

1)множества четных и натуральных чисел;

2)множества натуральных и рациональных чисел;

3)множества точек расположенных на двух различных отрезках (окружностях, квадратах);

4)равночисленные конечные множества;

5)множество точек на единичном отрезке координатной прямой и всей этой прямой.

Контрольные вопросы

1. Дать определение множества.

2. Что называют подмножеством?

3. Какие множества можно считать эквивалентными?

4. Перечислить бинарные операции, заданные для двух множеств.

5. Что называют декартовым произведением двух множеств?