Теорема Эйлера. Операции над графами

Теорема (Эйлера.)Связный плоский граф с 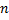вершинами и 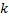ребрами разбивает плоскость на 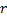областей (включая внешнюю), причем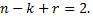

Путь называются Эйлеровым путем, если он содержит (проходит через) все ребра только один раз.

Граф, обладающий Эйлеро­вым циклом, называется эйлеровым или уникальным графом.

Плоские Эйлеровы графы можно изобразить одним росчерком пера, причем процесс изоб­ражения начинается и заканчивается в одной вершине.

Теорема.Граф 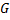является Эйлеровым тогда и только тогда, когда 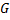– связный граф, имеющий все четные вершины.

Для установления факта является ли граф уникальным, досрочно установить факт четности всех вершин графа.

Гамильтоновым путем (циклом)графа 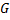называется путь (цикл), который проходит через каждую его вершину только один раз.

Граф, содержа­щий гамильтонов цикл, называется гамильтоновым.

Операции над графами.

Над графами, как и над любыми множествами можно выполнять операции объединения и пересечения.

Объединением графов 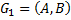и называется граф 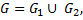множество вершин которого , а мно­жество ребер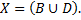

Пересечением графов 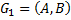и называется граф 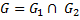, множество вершин которого 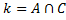, а мно­жество ребер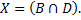

Подграфом данного графа называется граф все вершины и ребра, которого являются подмно­жествами множества вершин и ребер этого графа.

Обозначения подграфа, его вершин и ребер можно так, как это принято для обозначения подмножеств или ввести другие буквы.