Способы задания графов
Способы задания графа. Изоморфные графы.
Графы могут задаваться следующими способами:
1) геометрическим способом – рисунки, схемы, диаграммы;
2) алгебраическим способом – перечислением вершин и ребер;
3) табличным способом;
4) матричным способом.
Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в наглядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа называется его реализацией.
Для машинной обработки удобнее задать граф в алгебраической форме – перечислением (списком) вершин или ребер.
При переходе от алгебраического способа к геометрическому одному и тому же графу могут соответствовать различные изображения – изоморфные графы,при этом от правильного изображения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф.
Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несимметрично, во-вторых, для указания каждого ребра нужно еще раз выписывать соответствующие вершины, что плохо с точки зрения сжатия и хранения информации.
При задании графа таблицейсоставляется таблица,состоящей из 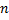 строк (вершины) и т
строк (вершины) и т  столбцов (ребра). На пересечении строк и столбцов пишутся соответствующие знаки, которые показывают отношение (инцидентность) вершины и ребра. Это может быть знаки “+” и “-”, числа 0,1,-1 и др.
столбцов (ребра). На пересечении строк и столбцов пишутся соответствующие знаки, которые показывают отношение (инцидентность) вершины и ребра. Это может быть знаки “+” и “-”, числа 0,1,-1 и др.
Главным во всех способах задания графа (диаграммой, матрицей, таблицей) является указание соответствия между множествами  вершин
вершин 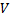 t к
t к  ребер
ребер 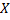 .
.
Пусть дан граф 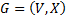 ,где
,где 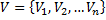 – вершины, а
– вершины, а 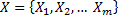 – ребра, среди которых могут и кратные ребра (есть вершины, которые соединяет несколько ребер).
– ребра, среди которых могут и кратные ребра (есть вершины, которые соединяет несколько ребер).
Матрицей инцидентностиданного графа будет таблица, состоящая из 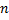 строк (вершины) и
строк (вершины) и 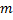 столбцов (ребра).
столбцов (ребра).
При рассмотрении неориентированного графа на пересечении строк и столбцов ставится число 1, если соответствующие вершина и ребро инцидентны и ставится число 0, они не инцидентны.
При рассмотрении ориентированного графа на пересечении строк и столбцов ставится число 1, если из вершины выходит соответствующее ее ребро. Если в вершину входит ребро, то ставят число -1. Если вершина не инцидентна ребру, то ставится число 0.
Очевидно, что в каждом столбце матрицы инцидентности должно быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки – степень соответствующей вершины.
Матрицы инцидентности прямоугольные, если число строк и столбцов различно. Если число вершин и ребер в графе одинаковое, то получается квадратная матрица.
Матрицу можно сделать квадратной для любого графа без кратных ребер. В таких случаях строки и столбцы изображают вершины. На пересечении строк и столбцов ставится число 1, если соответствующие вершины соединены ребром и ставится число 0, если вершины не соединены.
Для неориентированного графа ребраодновременно принадлежат или не принадлежат графу, так как символизируют одно и то же ребро. Матрица смежности неориентированного графа является симметрической и не меняется при транспонировании.
Хотя формально каждая вершина всегда смежная сама с собой, в матрице смежности мы будем ставить 0, если у нее нет петли, и 1, если есть одна петля.
Если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули.
Пример.Составить таблицу инцидентности для орграфа, который имеет 3 вершины и 4 ребра.
Таблица 8
| Вершины | Ребра | |||
| s | t | г | и | |
| V1 | -1 | |||
| V2 | -1 | |||
| V3 | -1 | -1 |
Граф называется взвешеннымили сетью,если каждому его ребру поставлено в соответствие некоторое число. Взвешенными графами могут быть схемы в электронике, электрические схемы, карты автомобильных и железных дорог и др. Например, на картах автодорог вершины являются населенными пунктами, ребра – дорогами, а весом – числа, равные расстоянию между населенными пунктами.
В основе процесса планирования лежит некоторый сценарий, представляющий собой сеть, состоящую из вершин – пошагового описания действий и дуг – отношений между ними. Такой граф дает возможность, сравнивая альтернативы, планировать действия для достижения поставленной цели.
Понятия-объекты и другие элементы предметной области могут быть графически изображены в виде вершин, а отношения между ними – в виде дуг, связывающих эти вершины.
Дата добавления: 2015-08-11; просмотров: 2668;
