Сочетания. Размещения. Перестановки

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

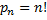
Где ( ).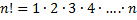

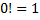Рассмотрим пример: сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?

Решение:

.

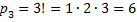Или такой пример. Порядок выступления семи участников на студенческой конференции определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение: каждый вариант жеребьевки отличается только порядком участников, то есть является перестановкой из 7 элементов. Их число находится

.

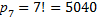Пример. К кассе за получением денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?

Решение: очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырех человек, их число равно

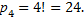
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо их порядком, либо составом элементов.

Число всех возможных размещений рассчитывается

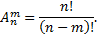
Пример: сколько можно составить сигналов из 6 флажков различного цвета, взятых по два?

Решение:

Пример: расписание одного дня состоит из пяти уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение: каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания находят по формуле

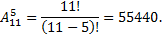
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

Пример: сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Решение:

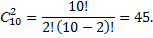
Пример: в шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение: каждая партия играется двумя участниками из 16 и отличается только составом пар участников, то есть представляет собой сочетание из 16 элементов по два

Пример: имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать три штамма. Сколькими способами можно это сделать?

Решение: способы отбора считаются различными, если каждый отобранный штамм различается хотя бы одним элементом. Это число

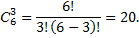
То есть имеется 20 способов.

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

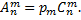
При решении задач комбинаторики используют следующие правила.

Правило суммы: если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно 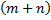способами.

Правило произведения: если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А,В) в указанном порядке может быть выбрана 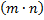способами.

Пример: в студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

Решение: по правилу умножения двух девушек можно выбрать 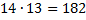способами, а двух юношей 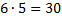способами. Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Согласно правилу сложения таких способов выбора будет 182 + 30 = 212.

Контрольные вопросы

1. Что называют графом?

2. Какие вершины графа можно назвать смежными?

3. Возможно ли начертить граф с нечетным числом нечетных вершин?

4. Чем определяется полный граф?

5. Что называют перестановками, размещениями, сочетаниями?

6. Сформулировать правила суммы и произведения.