Виды случайных событий

Часто вычисление вероятностей связано с рассмотрением ряда различных событий. Поэтому одним из основных понятий теории вероятностей является понятие события.

Случайным событием называется любой факт, который в результате испытания может произойти или не произойти.

Под испытанием в этом определении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание может осуществляться человеком, но может проводиться и независимо от человека, выступающего в роли наблюдателя.

Событие - это не какое-нибудь происшествие, а лишь возможный исход, результат испытания. События обозначаются прописными латинскими буквами: А, В, С.

Если при каждом испытании, при котором происходит событие А, происходит и событие В, то говорят, что А влечет за собой В или В включает событие А и обозначают .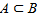

Если одновременно то в этом случае событие А и В называются равносильными.

События называются несовместными, если наступление одного из них исключает наступление любого другого в одном и том же испытании. В противном случае события называются совместными. Например, получение студентом на экзамене по одной дисциплине оценок "отлично", "хорошо" и "удовлетворительно" – события несовместные, а получение тех же оценок на экзаменах по трем дисциплинам - события совместные.

Событие называется достоверным, если в результате испытания оно обязательно должно произойти.

Событие называется невозможным, если в результате испытания оно вообще не может произойти. Например, в партии все изделия стандартные, то извлечение из нее стандартного изделия – событие достоверное, а извлечение при тех же условиях бракованного изделия - событие невозможное.

События называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не является объективно возможным.

Два события являются взаимоисключающими, если отсутствует возможность их одновременного наступления.

Независимые друг от друга события. Два события не зависят друг от друга, если каждое из них полностью не зависит от факта наступления другого.