Алгебра событий. алгебра событий.

Пусть - конечное пространство элементарных событий. Рассмотрим множество , состоящее из всех подмножеств множества 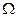. Оно содержит 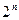элементов. Например, если 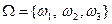, то 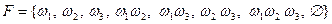. Пусть над элементами, входящими в определены операции сложения, умножения и вычитания. Тогда обладает следующими свойствами:

1) 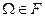, т.е. достоверное событие входит в .

2) замкнуто относительно операций сложения и умножения, т.е. .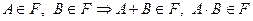

3) .

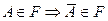В этом случае система множеств образует алгебру. Следовательно, случайные события образуют алгебру, если число исходов стохастического эксперимента конечно.

Пусть 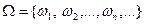-– бесконечное, но счетное пространство элементарных событий. Рассмотрим множество , состоящее из всех подмножеств множества 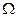. Пусть над элементами, входящими в определены операции сложения, умножения и вычитания. Тогда обладает следующими свойствами:

1) 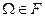, т.е. достоверное событие входит в .

2) замкнуто относительно операций сложения и умножения счетного множества событий, т.е. .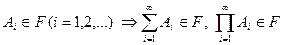

3) .

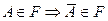В этом случае система множеств образует 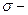алгебру. Следовательно, случайные события образуют 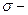алгебру, если число исходов стохастического эксперимента счетно.

Для несчетного 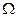событиями будем считать не все его подмножества, а только подмножества, которые образуют 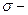алгебру.

Для любого пространства элементарных событий 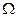, конечного, счетного или несчётного, будем называть событиями те и только те его подмножества, которые образуют алгебру или 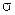– алгебру.