Алгебра логики

Алгебра логики – это раздел математики, занимающийся исчислением высказываний. Под высказыванием Х понимается любое предложение, относительно которого можно утверждать ложно оно или истинно без учёта конкретного содержания. Переменная величина, которая устанавливает лишь два значения 1 и 0, называется двоичной. Функция, определяемая набором двоичных аргументов и принимающая лишь два значения 1 или 0, называется функцией алгебры логики.

В алгебре логики рассматриваются три основные логические операции:

а) НЕ – отрицание. Отрицание высказывания Х обозначается 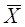и значения истинности определяются соотношениями

;

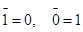б) И-конъюнкция. Конъюнкция (логическое умножение) высказываний Х 1 и Х 2 истинна тогда и только тогда, когда истинны составляющие её высказываний Х 1 и Х 2. Значения истинности конъюнкции определяются соотношениями

0  0=0, 0 1=0, 1  0=0, 1  1 = 1.

в) ИЛИ – дизъюнкция. Дизъюнкция (логическое сложение) высказываний Х 1 и Х 2 ложна тогда и только тогда, когда ложны составляющие её высказывания Х 1 и Х 2 . Значения истинности дизъюнкции определяются соотношениями

0+0=0, 0+1=1, 1+0=1, 1+1=1.

Основные правила преобразования:

X  1=X, X+1=1, X+0=X, X  0=0,

X  X=X, X+X=X, X 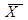 =0, X+ 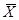=1.

Ассоциативный закон

Х 1  (Х 2  Х 3)=(Х 1  Х 2)  Х 3=Х 1  Х 2  Х 3.

Х 1+(Х 2+Х 3)=(Х 1+Х 2)+Х 3=Х 1+Х 2+Х 3.

Коммутативный закон

Х 1  Х 2=Х 2  Х 1,

Х 1+Х 2=Х 2+Х 1.

Дистрибутивный закон

Х 1  (Х 2+Х 3)=Х 1  Х 2+Х 1  Х 3,

Х 1+(Х 2  Х 3)=(Х 1+Х 2)  (Х 1+Х 3).

Закон инверсий

,

.

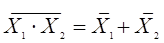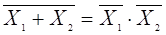Операция поглощения

Х 1+Х 1  Х 2=Х 1 Х 1  (Х 1+Х 2)=Х 1.