Алгебра множин

Операції над множинами, як і операції над числами, мають деякі властивості (табл.). Останні виражаються сукупністю тотожностей незалежно від конкретних множин, що входять у ці тотожності та є підмножинами деякого універсуму U.

Таблиця

Комутативність
1а) А È В = В È А	1б) А Ç В = В Ç А
Асоціативність
2а) А È (В È С) = (А È В) È С	2б) А Ç (В Ç С) = (А Ç В) Ç С
Дистрибутивність
3а) А È (В Ç С) = (А È В) Ç (А È С)	3б) А Ç (В È С) = (А Ç В) È (А Ç С)
Властивості порожньої множини Æ та універсуму U
4а) А È Æ = A	4б) А Ç U = A
5а)	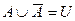5б)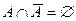
6а) А È U = U	6б) А Ç Æ = Æ
7а)	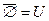7б)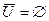
Самопоглинання
8а) А È A = A	8б) А Ç A = A
Поглинання
9а) А È (А Ç В) = А	9б) А Ç (А È В) = А
Правило де Моргана
10а)	10б)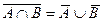
Властивості доповнення, різниці, диз’юнктивної суми
11)
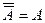
12)
13)
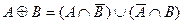
14) А Å В = В Å А
15) А Å (В Å С) = (А Å В) Å С
16) А Å Æ = Æ Å A = A

Основний метод доведення тотожностей в алгебрі множин ґрунтується на згаданому раніше факті: А = В тоді і тільки тоді, коли А Í В і В Í А. Доведемо, наприклад, тотожність 3а) А È (В Ç С) = (А È В) Ç (А È С).

Доведемо спочатку, що А È (В Ç С) Ì (А È В) Ç (А È С). Для цього візьмемо будь-яке x Î А È (В Ç С), тоді за означенням операцій È та Ç маємо x Î А або (x Î В і x Î С). За законом дистрибутивності “або” відносно “і” (x Î А або x Î В) і (x Î А або x Î С), тобто x Î А È В і x Î А È С. Це рівносильно x Î ( А È В) Ç (А È С), що й треба було довести.

Доведемо тепер, що (А È В) Ç (А È С) Ì А È (В Ç С). Для цього візьмемо будь-яке x Î (А È В) Ç (А È С). Звідси (x Î А або x Î В) і (x Î А або x Î С). Це рівносильно x Î А або (x Î В і x Î С), тобто x Î А È (В Ç С), що й потрібно було довести.

Таким чином, А È (В Ç С) = (А È В) Ç (А È С).

Із властивості асоціативності операції об’єднання множин випливає, що об’єднання кількох множин можна виконати, послідовно об’єднуючи їх, причому порядок входження множин не впливає на результат: А È (В È С) = (А È В) È С = А È В È С. Отже, об’єднання сукупності множин можна подати співвідношенням: .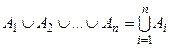

Аналогічно на n множин узагальнюється операція перетину: .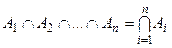

Використовуючи узагальнення операцій об’єднання та перерізу на n множин, можна узагальнити також інші співвідношення, наприклад закон де Моргана, який в узагальненому вигляді записується так: 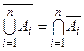і .

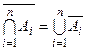Зауважимо, що операція декартового добутку неасоціативна і некомутативна, тобто множини (A´B)´C і A´(B´C), а також множини A´B і B´A, взагалі кажучи, не рівні між собою.

Зв’язок декартового добутку з іншими операціями над множинами встановлюється такими тотожностями:

(A È B) ´ C = (A´C) È (B´C),

(AÇB) ´ C = (A´C)Ç(B´C),

A ´ (B È C) =(A´B) È (A´C),

A ´ (BÇC) =(A´B)Ç(A´C).

Сукупність підмножин A₁, A₂, …, A_n множини A називається розбиттям множини A, якщо:

1. ;

2. A_i Ç A_j = Æ, i, j=1,.., n, i ¹ j.