Операції над множинами

Розглянемо дві множини А і В та введемо низку операцій над ними. Для графічної ілюстрації використовують діаграми (кола) Ейлера. Для зображення множини на площині креслять замкнену лінію із заштрихованою внутрішньою областю (найчастіше – це коло, звідси й назва відповідного інструмента, що широко застосовується в теорії множин).

Об’єднання А і В – множина, що складається з усіх елементів множини А, всіх елементів множини В і не містить ніяких інших елементів (рис. 1), тобто

А È В = {x | x Î А або x Î В}.

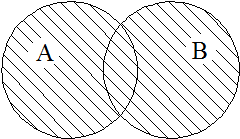
Рис. 1

Перетин А і В – множина, що складається з тих і тільки з тих елементів, які належать одночасно множині А та множині В (рис. 2), тобто

А Ç В = {x | x Î А і x Î В}.

Рис. 2

Різниця А і В (відносне доповнення) – множина, що складається з тих і тільки тих елементів, які належать множині А й не належать множині В (рис. 3), тобто

А \ В = {x | x Î А і x Ï В}.

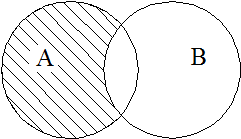
Рис. 3

Диз’юнктивна сума А і В (симетрична різниця) – множина, що складається усіх елементів А, які не належать множині В, й усіх елементів В, які не належать множині А, та яка не містить ніяких інших елементів (рис. 4), тобто

А Å В = {x | (x Î А і x Ï В) або (x Î В і x Ï А)}.

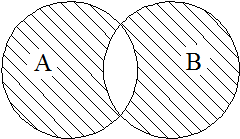
Рис. 4

Доповнення множини.

Звичайно, вже в означенні конкретної множини явно або неявно обмежується сукупність об’єктів, що є допустимими (слони – серед тварин, натуральні числа – серед цілих або дійсних залежно від контексту). Зручно сукупність допустимих об’єктів зафіксувати явно та вважати, що множини, які розглядаються, складаються з елементів цієї сукупності. Її називають основною множиною (універсумом) і позначають U. Універсум U арифметики – числа, універсум U зоології – тварини і т.д. Будь-яку множину розглядатимемо у зв’язку з універсумом, який на діаграмах Ейлера асоціюватимемо з прямокутником на площині, всередині якого зображатимемо множини (рис. 5).

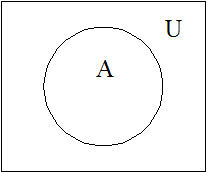
Рис. 5

Доповнення множини А – це множина, що містить усі елементи універсуму, за винятком елементів А (рис. 6), тобто .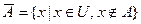

Рис.6

Множина А називається підмножиною множини В, якщо кожен елемент А є елементом В. Для позначення цього факту вводиться знак Ì - символ строгого включення (або Í - символ нестрогого включення) (рис. 7). Якщо необхідно підкреслити, що множина В містить також інші елементи, крім елементів множини А, то використовують символ строгого включення А Ì В.

Дві множини рівні, якщо вони складаються з одних і тих самих елементів. Справджується таке: А = В тоді і тільки тоді, коли А Í В і В Í А.

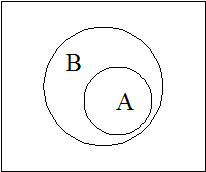
Рис. 7

Окремо розглянемо ще одну дуже важливу операцію над множинами.

Декартовим (прямим) добутком множин A і B (записується A´B) називається множина всіх пар (a,b), в яких перша компонента належить множині A (aÎA), а друга - множині B (bÎB).

Тобто

A´B = {(a,b) | aÎA і bÎB }

Декартовий добуток природно узагальнюється на випадок довільної скінченної сукупності множин. Якщо A₁, A₂,..., A_n - множини, то їхнім декартовим добутком називається множина

D = { (a₁,a₂,...,a_n) | a₁ÎA₁, a₂ÎA₂,..., a_nÎA_n },

яка складається з усіх наборів (a₁,a₂,...,a_n), в кожному з яких i-й член, що називається i-ю координатою або i-ю компонентою набору, належить множині A_i, i=1,2,...,n. Декартовий добуток позначається через A₁´ A₂´...´ A_n.

Набір (a₁,a₂,...,a_n), щоб відрізнити його від множини, яка складається з елементів a₁,a₂,...,a_n, записують не у фігурних, а в круглих дужках і називають кортежем, вектором або впорядкованим набором. Довжиною кортежу називають кількість його координат. Два кортежі (a₁,a₂,...,a_n) і (b₁,b₂,...,b_n) однакової довжини вважаються рівнимитоді і тільки тоді, коли рівні їхні відповідні координати, тобто a_i=b_i, i=1,2,...,n. Отже, набори (a,b,c) і (a,c,b) вважаються різними, в той час як множини {a,b,c} і {a,c,b} - рівні між собою.

Декартовий добуток множини A на себе n разів, тобто множину A´A´...´A називають n-м декартовим (або прямим) степенем множини A і позначають Aⁿ.

Прийнято вважати, що A⁰ = Æ (n=0) і A¹ = A (n=1).

Наприклад, якщо A = {a,b} і B = {b,c,d}, то

A´B = {(a,b),(a,c),(a,d),(b,b),(b,c),(b,d)},

A² = {(a,a),(a,b),(b,a),(b,b)}.

Якщо R - множина дійсних чисел або множина точок координатної прямої, то R² - це множина пар (a,b), де a,bÎR, або множина точок координатної площини.

Координатне зображення точок площини вперше було запропоновано французьким математиком і філософом Рене Декартом, тому введена операція над множинами і називається декартовим добутком.

Множину, елементами якої є всі підмножини множини А, називають множиною підмножин множини А (або булеаном множини А) і позначають Р(А). Так, для триелементної множини А = {a, b, c} маємо P(A)={Æ, {a}, {b}, {c}, {a, b},{b, c}, {a, c}, {a, b, c}}. У разі скінченної множини А з n елементів, множина підмножин Р(А) містить 2ⁿ елементів.