Вероятностное пространство эксперимента с конечным числом исходов. Вероятность события.
Пусть 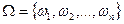 - пространство элементарных событий с конечным числом исходов. Событием является любое подмножество множества
- пространство элементарных событий с конечным числом исходов. Событием является любое подмножество множества 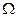 . Пусть
. Пусть  – соответствующая алгебра событий. Основной числовой характеристикой случайного события является его вероятность. Вероятность события – количественная мера объективной возможности наступления события. Вероятность является объективным свойством , которое не зависит от того, проводился опыт или нет. Например, вероятность выпадения герба присуща данной монете, как и ее масса, размер и т.д. Если монета симметрична, то можно предположить, что вероятность выпадения герба равна 1/2, однако правильность такого предположения проверяется в результате большого числа опытов.
– соответствующая алгебра событий. Основной числовой характеристикой случайного события является его вероятность. Вероятность события – количественная мера объективной возможности наступления события. Вероятность является объективным свойством , которое не зависит от того, проводился опыт или нет. Например, вероятность выпадения герба присуща данной монете, как и ее масса, размер и т.д. Если монета симметрична, то можно предположить, что вероятность выпадения герба равна 1/2, однако правильность такого предположения проверяется в результате большого числа опытов.
Каждому элементарному событию 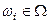 (исходу эксперимента) аксиоматически приписывают число
(исходу эксперимента) аксиоматически приписывают число 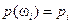 , называемое вероятностью этого исхода, т.е. на
, называемое вероятностью этого исхода, т.е. на 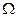 задается числовая функция
задается числовая функция 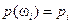 , которая должна удовлетворять условиям:
, которая должна удовлетворять условиям:
1. 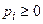 для любого
для любого  – аксиома неотрицательности;
– аксиома неотрицательности;
2. 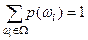 (или
(или 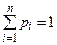 , где
, где  – количество элементарных событий) – аксиома нормированности.
– количество элементарных событий) – аксиома нормированности.
Вероятностью произвольного события  называется сумма вероятностей исходов, входящих в
называется сумма вероятностей исходов, входящих в  .
.
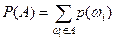 .
.
Это равенство определяет вероятность как функцию, заданную на алгебре событий  . Она обладает следующими свойствами
. Она обладает следующими свойствами
1) 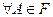
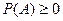 .
.
Действительно, 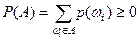 , так как
, так как 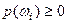 .
.
2) 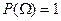 ,т.е. вероятность достоверного события равна 1. Это следует из из условия нормированности
,т.е. вероятность достоверного события равна 1. Это следует из из условия нормированности 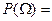
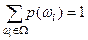 .
.
3) Если  и
и 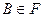 , причем
, причем 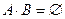 , (т.е. события несовместны),.то
, (т.е. события несовместны),.то 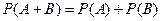 – свойство аддитивности.
– свойство аддитивности.
Действительно, 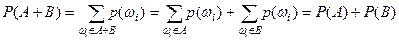 .
.
Следовательно, вероятность – неотрицательная, нормированная , аддитивная числовая функция, заданная на множестве  .
.
Для эксперимента с конечным числом исходов вероятностная модель считается построенной, если
1) указано пространство 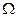 элементарных событий, которое определяет алгебру
элементарных событий, которое определяет алгебру  ;
;
2) . Каждому элементарному событию 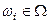 (исходу эксперимента) приписана вероятность
(исходу эксперимента) приписана вероятность 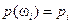 , удовлетворяющая двум аксиомам.
, удовлетворяющая двум аксиомам.
Тройка 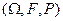 называется вероятностным пространством. Алгебра
называется вероятностным пространством. Алгебра  является областью определения вероятностей событий
является областью определения вероятностей событий 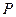 .
.
Вероятностное пространство эксперимента называют вероятностной моделью эксперимента.
Часто вероятностное пространство задают в виде таблицы.
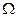
| 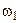
| 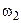
| … | 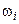
| … | 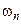
|
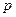
| 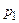
| 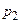
| … | 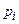
| … | 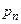
|
Теория вероятности не дает ответа на вопрос о том, как правильно определить вероятности 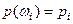 элементарных событий. На этот вопрос отвечает математическая статистика. При определении этих вероятностей принимается во внимание интуитивное представление о
элементарных событий. На этот вопрос отвечает математическая статистика. При определении этих вероятностей принимается во внимание интуитивное представление о 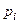 как о частоте элементарного события
как о частоте элементарного события 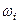 в серии большого числа испытаний.
в серии большого числа испытаний.
Дата добавления: 2015-08-21; просмотров: 3008;
