Классическое определение вероятности
Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Мы с Вами будем опираться на определение, которое называют классическим.
Рассмотрим пример. Пусть в урне содержится 6 одинаковых шарика, причем 2 из них – красные, 3 – синие и 1 – белый. Очевидно, возможность вынуть наудачу из урны цветной (т.е. красный или синий) шар больше, чем возможность извлечь белый шар.
Можно ли охарактеризовать эту возможность числом? Оказывается можно. Это число и называют вероятностью события (появления цветного шара).
Вероятность есть число, характеризующее степень возможности появления события.
Дадим количественную оценку возможности того, что взятый наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события А.
Заметим, что событие – это результат испытания (законченное действие); испытание – это совокупность условий, при осуществлении которых случайное событие может произойти, либо не произойти. Каждый из возможных результатов испытания назовем элементарным исходом (элементарным событием).
В нашем примере возможны следующие 6 элементарных исходов: 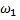 – появился белый шар;
– появился белый шар; 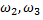 – появился красный шар;
– появился красный шар; 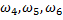 – появился синий шар. Данные события образуют полную группу, т.к. в результате испытания появится хотя бы одно из них и они равновозможны (т.к. шары тщательно перемешаны). Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем случае:
– появился синий шар. Данные события образуют полную группу, т.к. в результате испытания появится хотя бы одно из них и они равновозможны (т.к. шары тщательно перемешаны). Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем случае: 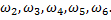
Отношение числа благоприятствующих событию А элементарных, равновозможных исходов к их общему числу называют вероятностью события А и обозначают Р(А)
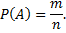
Здесь предполагается, что элементарные исходы несовместны, равновозможны.
Из определения вероятности следуют следующие свойства:
1) вероятность достоверного события равна единице

2) вероятность невозможного события равна нулю
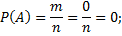
3) вероятность случайного события есть величина положительная, заключенная между нулем и единицей
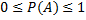 .
.
Дата добавления: 2015-08-11; просмотров: 1046;
