Множества. Под множеством можно понимать неупорядоченную совокупность элементов, набор объектов

Под множеством можно понимать неупорядоченную совокупность элементов, набор объектов. Примерами множеств может служить:

1) множество людей, например, группа детей одного класса – элементами служат учащиеся именно данного класса;

2) совокупность всех классов некоторой школы – элементами являются именно группы детей, образующих каждый их этих классов;

3) множество натуральных чисел: натуральные числа – числа от 1 до бесконечности;

4) множество треугольников: любой треугольник является элементом этого класса;

5) D= {2, 4, 6, 8, 10, 12…} – множество четных чисел.

Если множество задано, каждый элемент его уникален, т. е. отличим от других; причем для любого объекта существует возможность установить, принадлежит ли он множеству или нет.

Множества обозначаются заглавными буквами, как правило, латинского алфавита. При этом элементы множества принято заключать в фигурные скобки.

Принадлежность элемента множеству обозначается символом , например, 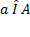, не принадлежность символом .

Например, рассмотрим множество 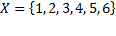. Запись 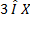, означает, что число 3 принадлежит множеству , , 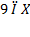что число 9 не принадлежит множеству .

Совокупность 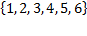является множеством, последовательность записи элементов не имеет значения, поэтому оно неотличимо от множества

Совокупность 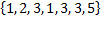множеством не является, здесь некоторые элементы записаны не единичным образом.

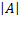Число элементов множества обозначается, как и называется мощностью или численностью (размером, нормой, длиной и др.) множества.

Множество, не содержащее элементов, обозначается символом 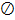и называется пустым множеством. Пустое множество может встретиться в реальных задачах. Так, например, может оказаться, что множество студентов группы, получивших две неудовлетворительные оценки, пусто. Это значит, что таковых студентов нет.

Множество может быть представлено в виде:

- перечисления, например, ,

- свойства, например, 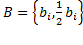– студенты старше 25 лет,

- процедуры, например, .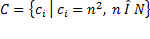

Здесь и далее при задании множества символ – вертикальная разделительная черта, используется вместо слов “таких, что”, “всех” и др.

Рассмотрим запись которая означает, что множество 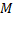состоит их всех элементов , обладающих свойством .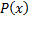

Например, запись означает, что множеству 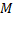принадлежат корни уравнения .

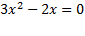При задании множества используют новые символы и слова:

- , для обозначения союза “И”

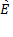- для обозначения союза “ИЛИ”

- ” квантор общности, для обозначения слов: “для всех”, “для каждого”…

- $ квантор существования, для обозначения слов: “существует”, ”найдется” ….

Свойство, с помощью которого задано множество, называется характеристическим свойством. Этим свойством должны обладать все элементы данного множества. А именно, все элементы заданного множества обладают характеристическим свойством и если некоторый из элементов не принадлежат этому множеству, то он не обладают заданным свойством.

Для наглядности множества на плоскости изображаются кругами или иными плоскими геометрическими фигурами, замкнутыми контурами.