Определение ряда Фурье
Пусть 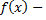 произвольная периодическая функция с периодом
произвольная периодическая функция с периодом 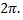 Предположим, что функция
Предположим, что функция  разлагается в тригонометрический ряд, т.е.
разлагается в тригонометрический ряд, т.е.  является суммой ряда
является суммой ряда
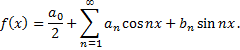
Так как функция  имеет период
имеет период 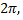 то ее можно рассматривать в любом промежутке длины
то ее можно рассматривать в любом промежутке длины 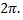 В качестве основного промежутка возьмем отрезок
В качестве основного промежутка возьмем отрезок 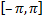 (также удобно взять отрезок
(также удобно взять отрезок 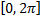 ) и предположим, что ряд
) и предположим, что ряд
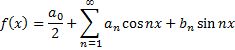
на этом отрезке можно почленно интегрировать. Вычислим коэффициенты 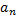 и
и 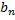 для этого проинтегрируем обе части равенства в пределах от
для этого проинтегрируем обе части равенства в пределах от 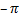 до
до 
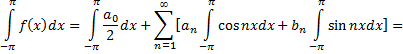
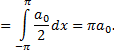
Интегралы от всех, кроме нулевого, членов ряда равны нулю. Отсюда
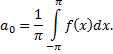
Умножив обе части равенства
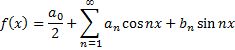
на 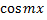 и проинтегрировав полученный ряд в пределах от
и проинтегрировав полученный ряд в пределах от 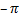 до
до  получим
получим
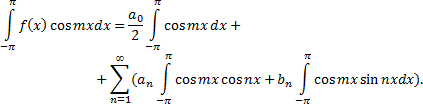
Из последнего равенства при 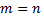 получаем
получаем
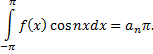
Отсюда
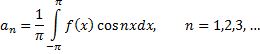
Аналогично, умножив равенство
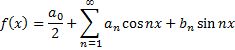
на  и проинтегрировав почленно на отрезке
и проинтегрировав почленно на отрезке 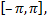 найдем
найдем
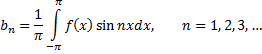
Числа 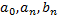 называются коэффициентами Фурье функции
называются коэффициентами Фурье функции 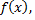 а тригонометрический ряд
а тригонометрический ряд
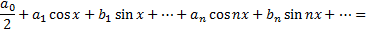
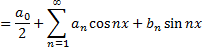
с такими коэффициентами – рядом Фурье функции 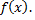 Для интегрируемой на отрезке
Для интегрируемой на отрезке 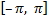 функции
функции  записывают
записывают
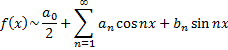
и говорят, что функции  соответствует ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначают
соответствует ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначают 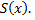
Дата добавления: 2015-08-11; просмотров: 762;
