Приложение рядов к приближенным вычислениям

Приближенное вычисление значений функции.

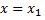Пусть требуется вычислить значение функции при с заданной точностью

Если функцию в интервале 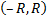можно разложить в степенной ряд

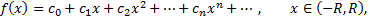
то точное значение 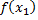равно сумме этого ряда при 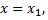т.е.

а приближенное значение – частичной сумме

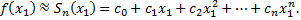
Точность этого равенства увеличивается с ростом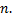

Рассмотрим пример. Вычислить приближенно с точностью до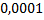

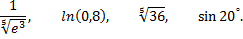
Для вычисления

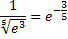
запишем ряд

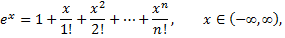
при 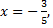принадлежащем области сходимости

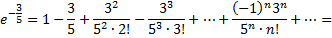
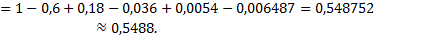
Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница для сходящегося ряда мы допустим погрешность, не превышающую первого отброшенного члена, т.е.

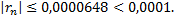
Итак,

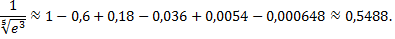
Для вычисления 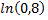запишем

при входящим в область сходимости ряда

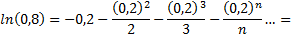
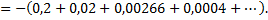
Если в качестве 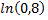взять первые четыре члена, мы допустим погрешность

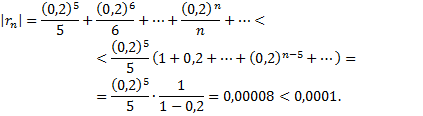
Итак,

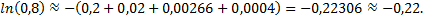
Представим 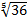в виде

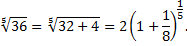
Так как 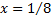входит в область сходимости степенного ряда 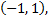то при

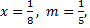
учитывая, что

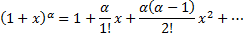
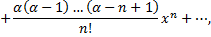
получим

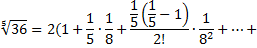
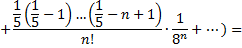
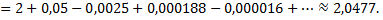
Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося ряда погрешность

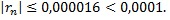
Для вычисления

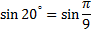
запишем ряд

при 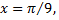принадлежащем области сходимости

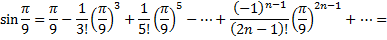
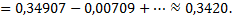
Необходимо взять два члена, так как при этом погрешность

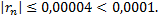
Итак,

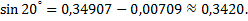
Приближенное вычисление определенных интегралов.

Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно.

Пусть требуется вычислить интеграл

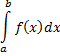
с точностью до Если подынтегральную функцию можно разложить в ряд по степеням и интеграл сходимости 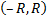включит в себя отрезок 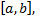то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.

Рассмотрим пример. Вычислить приближенно с точностью до

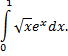
Точное интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив на 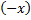в разложении

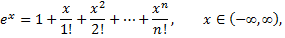
получим

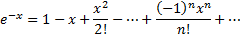
Умножая полученный ряд на 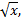получим

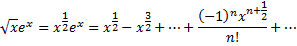
затем почленно интегрируя в интервале 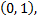принадлежащем интервалу сходимости ряда 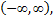получим

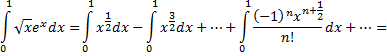
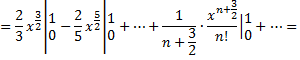
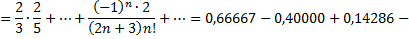
Оценка погрешности вычисления производится так же, как и в предыдущих примерах.

Приближенное решение дифференциальных уравнений.

Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора. Одним из способов решения дифференциальных уравнений с помощью степенных рядов, является способ последовательного дифференцирования. Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пусть, например, требуется решить уравнение

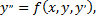
удовлетворяющее начальным условиям

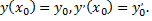
Решение 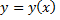уравнения

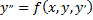
ищем в виде ряда Тейлора

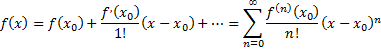
при этом первые два коэффициента находим из начальных условий

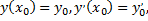
находим третий коэффициент

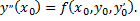
Значения

находим путем последовательного дифференцирования уравнения

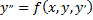
по и вычисления производных при 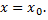Найденные значения производных подставляем в равенство

Этот ряд представляет искомое решение уравнения

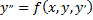
для тех значений при которых он сходится. Частная сумма этого ряда будет приближенным решением уравнения

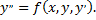
Рассмотрим пример. Методом последовательного дифференцирования найти 5 первых членов (отличных от нуля) разложения в ряд решения уравнения

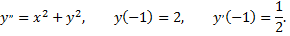
Будем искать решение уравнения в виде

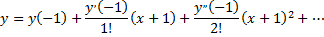
Здесь

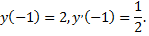
Находим 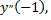подставив 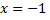в исходное уравнение

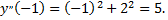
Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение

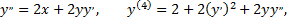
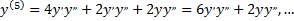
при 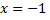имеем

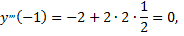
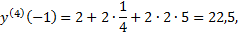
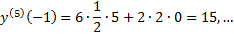
Подставляя найденные значения производных в искомый ряд, получим

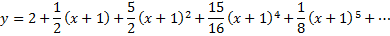
Контрольные вопросы

1. Привести примеры разложения в ряд Маклорена некоторых элементарных функций.

2. Сформулировать алгоритм приближенного вычисления определенных интегралов.

3. Сформулировать алгоритм приближенного решения дифференциального уравнения.