Теорема Абеля

Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.

Если степенной ряд сходится при значении 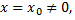то он сходится и, притом абсолютно, при всех значениях таких, что

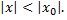
Если степенной ряд расходится при 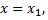то он расходится при всех значениях таких, что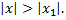

Из теоремы Абеля следует, что если 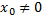есть точка сходимости степенного ряда, то интервал весь состоит из точек сходимости данного ряда, при всех значениях вне этого интервала ряд

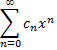
расходится.

Интервал 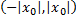называется интервалом сходимости степенного ряда. Положив 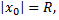интервал сходимости можно записать в виде 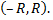Число называется радиусом сходимости степенного ряда, т.е. 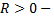это такое число, что при всех для которых

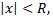рассматриваемый ряд абсолютно сходится, а при 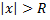ряд расходится.

На концах интервала радиуса сходимости, т.е. при 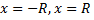сходимость ряда проверяется в каждом случае отдельно.

Найдем выражение радиуса сходимости степенного ряда

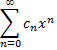
через его коэффициенты. Рассмотрим ряд, составленный из абсолютных величин его членов

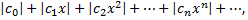
в котором все коэффициенты 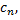по крайней мере, начиная с некоторого номера 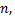отличны от нуля. По признаку Даламбера ряд сходится, если

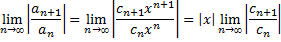
будет меньше единицы, т.е.

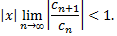
Радиус сходимости рассматриваемого ряда

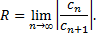
Рассмотрим пример. Найти область сходимости степенного ряда

Найдем радиус сходимости

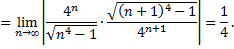
Следовательно, интервал сходимости

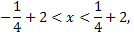
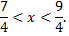
Исследуем сходимость ряда на концах интервала.

Пусть 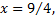тогда степенной ряд примет вид

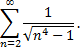
Сравним числовой ряд

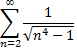
с обобщенно гармоническим рядом

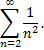
Применим признак сравнения

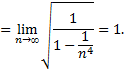
Так как предел конечен и отличен от нуля, то оба ряда сходятся или расходятся одновременно. Ряд

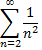
сходится, то сходится и ряд

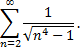
Следовательно, точка 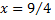принадлежит области сходимости.

Пусть 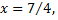тогда степенной ряд примет вид

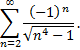
Это знакочередующийся ряд. Абсолютные величины членов этого ряда монотонно убывают и

По признаку Лейбница, ряд

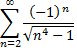
сходится. Следовательно, точка 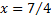принадлежит области сходимости.

Таким образом, областью сходимости степенного ряда

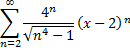
будет отрезок

Стоит отметить, что у некоторых рядов интервал сходимости вырождается в точку 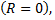у других охватывает всю числовую ось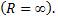

Степенной ряд в интервале его сходимости можно интегрировать и дифференцировать почленно. Его сумма является непрерывной функцией.

Рассмотрим пример. Найти область сходимости степенного ряда

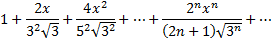
Найдем радиус сходимости ряда по формуле

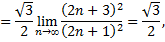
т.е. интервал сходимости ряда

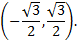
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 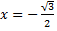данный степенной ряд принимает вид

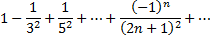
этот ряд сходится по признаку Лейбница.

На правом конце, при 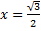получаем ряд

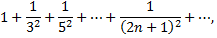
представляющий обобщенный гармонический ряд при 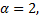у которого все члены с четными номерами равны нулю. Так как 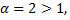то этот ряд сходится.

Итак, область сходимости данного ряда

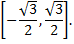
Контрольные вопросы

1. Дать определение степенного ряда.

2. Сформулировать теорему Абеля.

3. Как найти радиус сходимости степенного ряда?

4. Что называют областью сходимости степенного ряда?