Функциональные ряды
Ряд, членами которого являются функции от 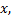 называется функциональным
называется функциональным

Придавая  определенное значение
определенное значение  получаем числовой ряд
получаем числовой ряд
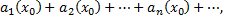
который может быть как сходящимся, так и расходящимся.
Если полученный числовой ряд сходится, то точка  называется точкой сходимости ряда
называется точкой сходимости ряда
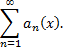
Если ряд расходится, то точка  называется точкой расходимости ряда
называется точкой расходимости ряда
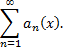
Совокупность числовых значений аргумента  при которых функциональный ряд сходится, называется его областью сходимости.
при которых функциональный ряд сходится, называется его областью сходимости.
В области сходимости функционального ряда его сумма является некоторой функцией от 

Определяется сумма в области сходимости равенством

где
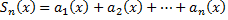
- частичная сумма.
Рассмотрим пример. Найти область сходимости ряда

Данный ряд является рядом геометрической прогрессии со знаменателем 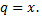 Следовательно, этот ряд сходится при
Следовательно, этот ряд сходится при 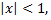 т.е. при всех
т.е. при всех 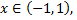 сумма ряда равна
сумма ряда равна
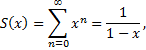
при 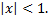
Рассмотрим пример. Исследовать сходимость функционального ряда
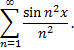
Составим ряд из абсолютных величин членов исходного ряда
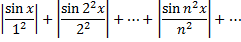
Так как при любом  имеет место соотношение
имеет место соотношение
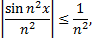
а ряд с общим членом  сходится, то по признаку сравнения ряд, состоящий из модулей, сходится при всех
сходится, то по признаку сравнения ряд, состоящий из модулей, сходится при всех 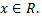
Дата добавления: 2015-08-11; просмотров: 1019;
