Достаточные признаки сходимости ряда
Сходимость и расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости ряда.
Рассмотрим эталонные ряды, которые часто используются при исследовании сходимости многих рядов.
Исследуем сходимость гармонического ряда
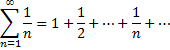
Гармонический ряд – это ряд, каждый член которого, начиная со второго, является средним гармоническим его соседних членов
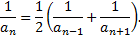
Его частичная сумма
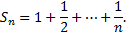
Пусть 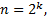 тогда
тогда
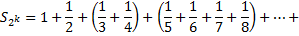
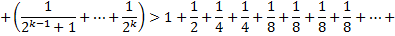
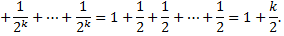
Таким образом,
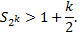
Последовательность 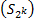 не ограничена сверху, а потому не может быть сходящейся, так как сходящаяся последовательность ограничена. Следовательно, ряд
не ограничена сверху, а потому не может быть сходящейся, так как сходящаяся последовательность ограничена. Следовательно, ряд
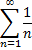
расходится.
Гармонический ряд расходится очень «медленно». Л. Эйлер, например, вычислил, что
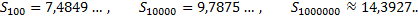
(Леонард Эйлер (1707-1783) – математик, физик, механик; родился в Швейцарии, большую часть жизни прожил в России и в Германии, активно участвовал во многих направлениях деятельности Петербургской и Берлинской академий.)
Рассмотрим пример. Ряд
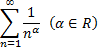
называется обобщенно гармоническим. При 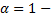 это гармонический ряд, и его расходимость доказана. Покажем, что этот ряд расходится и при
это гармонический ряд, и его расходимость доказана. Покажем, что этот ряд расходится и при 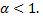
Здесь
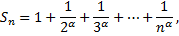
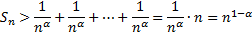
при любом 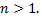 Следовательно
Следовательно
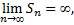
и поэтому при 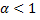 данный ряд расходится. Итак, обобщенный гармонический ряд расходится при
данный ряд расходится. Итак, обобщенный гармонический ряд расходится при 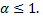
При 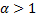 этот ряд сходится.
этот ряд сходится.
Рассмотрим пример. Исследуем на сходимость ряд
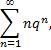
где 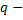 действительное число
действительное число 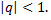
Преобразуем частичную сумму 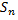 этого ряда следующим образом
этого ряда следующим образом
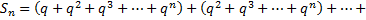
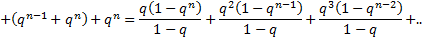
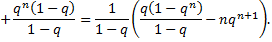
Отсюда
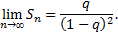
Следовательно, ряд
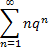
сходится и его сумма равна
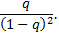
В частности, если
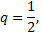
то
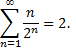
Признаки сравнения рядов.
Первый признак сравнения рядов. Пусть даны два ряда с положительными членами
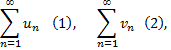
причем члены первого ряда не превосходят членов второго ряда, т.е. при любом 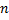
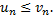
Тогда, если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).
Эталонные ряды, часто используемые для сравнения:
1) геометрический ряд
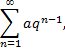
который сходится при 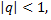 расходится при
расходится при 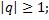
2) гармонический ряд
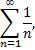
который расходится;
3) обобщенный гармонический ряд
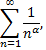
который сходится при 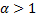 и расходится при
и расходится при 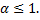
Рассмотрим пример. Исследовать сходимость ряда
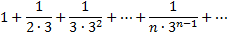
Сравним данный ряд со сходящимся геометрическим рядом
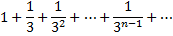
знаменатель, которого 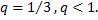
Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда
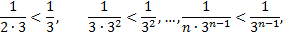
то на основании признака сравнения исследуемый ряд сходится.
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный ряд», но и доказать неравенство 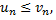 для чего часто требуется преобразование рядов.
для чего часто требуется преобразование рядов.
В ряде случаев более простым оказывается предельный признак сравнения.
Если рассматривают
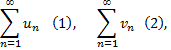
ряды с положительными членами, существует конечный предел отношения их общих членов
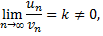
то ряды одновременно сходятся, либо одновременно расходятся.
Рассмотрим пример. Исследовать сходимость ряда
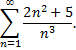
Сравним данный ряд с расходящимся гармоническим
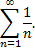
Так как
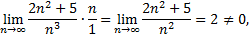
то данный ряд, так же как и гармонический, расходится.
Рассмотрим пример. Исследовать на сходимость ряд
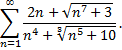
Подберем подходящий для сравнения эталонный ряд. Рассмотрим поведение числителя и знаменателя общего члена при 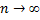
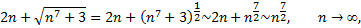
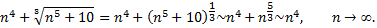
Возьмем
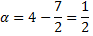
и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд
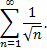
Найдем
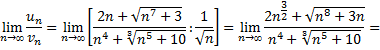
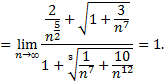
Предел конечен и отличен от нуля, условие предельного признака сравнения выполнено, значит, исходный ряд по предельному признаку сравнения тоже расходится.
Рассмотрим пример. Выяснить вопрос о сходимости ряда
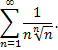
Ряд расходится, так как
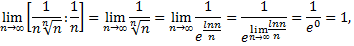
и гармонический ряд расходится.
Рассмотрим пример. Исследовать на сходимость ряд
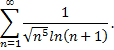
Так как предел отношения общих членов данного ряда и ряда
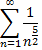
равен нулю
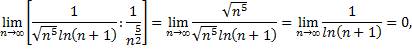
то по предельному признаку сравнения из сходимости ряда
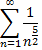
следует сходимость исходного ряда.
Признак Даламбера. (Жан Лерон  Ламбер (1717-1783) – один из самых разносторонних и влиятельных ученых Франции. Математик, физик, механик, а также автор ряда трудов по музыке и эстетике.)
Ламбер (1717-1783) – один из самых разносторонних и влиятельных ученых Франции. Математик, физик, механик, а также автор ряда трудов по музыке и эстетике.)
Пусть для ряда с положительными членами
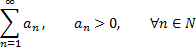
существует предел отношения 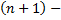 го члена к
го члена к 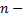 му члену
му члену
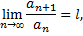
где  Тогда, если
Тогда, если 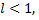 то ряд сходится, если
то ряд сходится, если 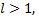 то ряд расходится, если
то ряд расходится, если 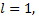 то вопрос о сходимости ряда остается открытым.
то вопрос о сходимости ряда остается открытым.
Рассмотрим пример. Исследовать сходимость ряда
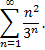
Данный ряд сходится, так как
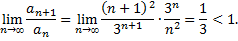
Рассмотрим пример. Исследуем на сходимость ряд
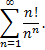
Имеем
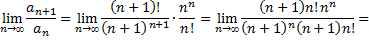
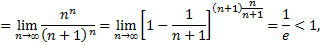
поэтому ряд сходится.
Рассмотрим пример. Исследовать сходимость ряда
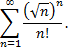
Имеем
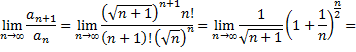
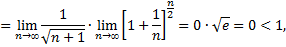
т.е. рассматриваемый ряд сходится.
Радикальный признак Коши. Признак Коши применяют для исследования знакоположительных рядов. Этот признак во многом схож с признаком Даламбера.
Пусть дан ряд
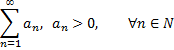
и существует конечный или бесконечный предел
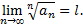
Тогда ряд сходится при 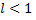 и расходится при
и расходится при 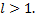 В случае, когда
В случае, когда 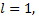 вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.
Рассмотрим пример. Исследуем сходимость ряда
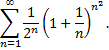
Имеем
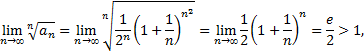
Следовательно по признаку Коши ряд расходится.
Интегральный признак Коши. Если члены знакоположительного ряда
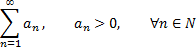
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 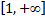 функции
функции  так, что
так, что
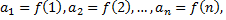
то:
1) если
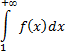
сходится, то сходится и знакоположительный исследуемый ряд;
2) если
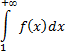
расходится, то расходится и знакоположительный исследуемый ряд.
Рассмотрим пример. Исследовать на сходимость ряд
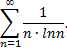
Воспользуемся интегральным признаком Коши. Функция
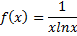
удовлетворяет условиям интегральной теоремы Коши. Находим
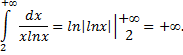
Так как несобственный интеграл расходится, то и исследуемый ряд так же расходится.
Контрольные вопросы
1. Что называют числовым рядом?
2. Пояснить понятие суммы ряда.
3. Перечислить свойства сходящихся рядов.
4. Записать необходимое условие сходимости числовых рядов.
5. Сформулировать достаточные условия сходимости рядов с неотрицательными членами.
Дата добавления: 2015-08-11; просмотров: 2248;
