Достаточный признак сходимости знакочередующихся рядов

Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно, то положительны, то отрицательны

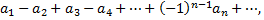
где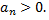

Признак Лейбница. Если члены знакочередующегося ряда убывают по абсолютной величине

и предел его общего члена при 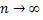равен нулю, т.е.

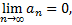
то ряд сходится, а его сумма не превосходит первого члена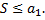

Замечание. В теореме Лейбница существенно не только условие

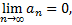
но и условие

Так, например, для ряда

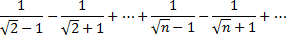
второе условие нарушено и, хотя

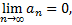
ряд расходится.

Следствие: погрешность при приближенном вычислении суммы сходящегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

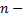Сумму сходящегося ряда можно представить как сумму членов ряда и суммы го остатка ряда, т.е. 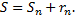Полагая приближенно 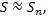мы допускаем погрешность, равную 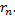Так как при четном 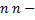й остаток знакочередующегося ряды 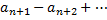представляет ряд, удовлетворяющий условиям теоремы Лейбница, то его сумма 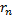не превосходит первого члена 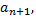т.е. 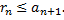Так как при нечетном для 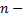го остатка ряда 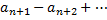его сумма 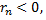то при любом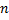

Рассмотрим пример. Исследовать сходимость ряда

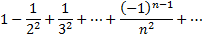
Так как члены знакочередующегося ряда убывают по абсолютной величине

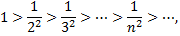
предел общего члена

то по признаку Лейбница ряд сходится.

Знакопеременные ряды. Пусть 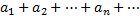знакопеременный ряд, в котором любой его член может быть как положительным, так и отрицательным.

Достаточный признак сходимости знакопеременного ряда.

Если ряд, составленный из абсолютных величин членов данного ряда

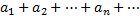
сходится, то сходится и данный ряд.