Необходимый признак сходимости ряда

Нахождение n-й частичной суммы 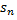и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них является необходимый признак сходимости.

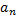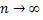Если ряд сходится, то предел его общего члена при равен нулю, т.е.

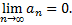
Рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если предел общего члена при 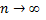равен нулю, то из этого не следует, что ряд сходится.

Следствием является достаточное условие расходимости ряда. Если

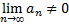
или этот предел не существует, то ряд расходится.

Рассмотрим пример. Выяснить вопрос о сходимости или расходимости ряда

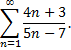
Предел общего члена ряда

т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится.