Задачи, приводящие к решению дифференциальных уравнений

Простейшие обыкновенные дифференциальные уравнения рассматривали в своих работах еще И. Ньютон и Г. Лейбниц. Именно Г. Лейбниц ввел в 1676 году термин «дифференциальные уравнения». Задачу решения обыкновенного дифференциального уравнения И. Ньютон трактовал как обратную по отношению к нахождению производной для заданной функции, а вычисление неопределенного интеграла он считал частным случаем этой задачи. Для Ньютона как создателя основ математического естествознания такой подход к восстановлению функции по зависимости между функцией и ее производными был вполне логичным, поскольку большинство известных в науке закономерностей может быть выражено в форме дифференциальных уравнений.

Рассмотрим пример. Тело массой падает под действием силы тяжести где 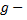ускорение свободного падения и силы сопротивления 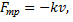пропорциональной скорости где коэффициент сопротивления. Найти зависимость скорости движения тела от времени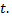

Используя второй закон Ньютона, составим обыкновенное дифференциальное уравнение, описывающее движение тела

Имеем дифференциальное уравнение первого порядка, разрешенное относительно производной 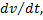имеющей механический смысл ускорения движения рассматриваемого тела. Можно проверить подстановкой, что решением этого обыкновенного дифференциального уравнения является совокупность функций

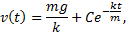
где 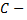произвольная постоянная.

Если в момент времени 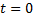тело начинает падение с начальной скоростью 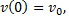то

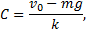
и тогда

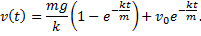
Кроме того, это обыкновенное дифференциальное уравнение имеет решение к которому стремятся при 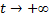все решения вне зависимости от значения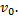

Рассмотрим пример. Из точки 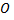под углом к горизонту бросают с заданной начальной скоростью 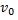тело массой 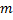так, что оно падает под прямым углом на наклонную плоскость, проходящую через точку 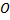и образующую с горизонтом заданный угол 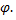Считая углы и 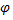острыми, найти угол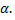

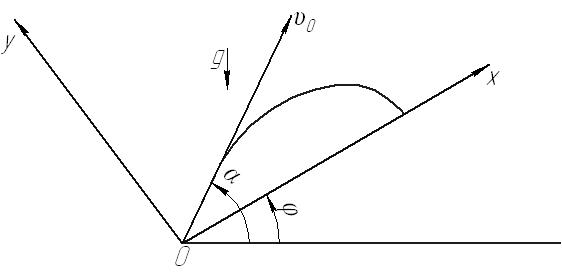
Рис. 64

Поместим в точку 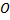начало прямоугольной декартовой системы координат, направив ось абсцисс 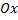вдоль наклонной плоскости. Согласно второму закону Ньютона, уравнения движения тела имеют вид:

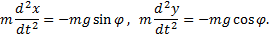
Это обыкновенные дифференциальные уравнения второго порядка, разрешенные относительно старшей производной. Они имеют решение:

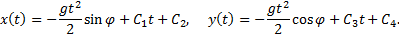
В уравнение входят четыре произвольных постоянных 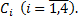Поэтому для выбора из бесконечного множества возможных решений единственного решения, описывающего действительное движение рассматриваемого тела, необходимо использовать сведения о положении и скорости тела в начальный момент времени однозначно определяющие эти произвольные постоянные. Так как при 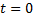тело находится в начале координат, т.е.

то,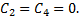

Дифференцируя, получаем

С учетом заданного при 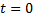значения 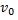скорости тела имеем

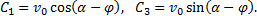
Подставляя найденные выражения для произвольных постоянных в

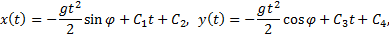
запишем

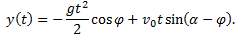
Полученное решение содержит пока еще неизвестное значение угла 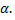Это значение можно найти, приняв во внимание, что тело падает на наклонную плоскость под прямым углом, т.е. в момент времени 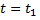падения 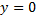и проекция скорости тела на координатную ось 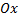равна нулю. Учитывая, что

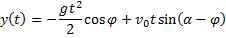
имеем

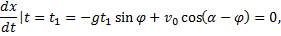
Из условия

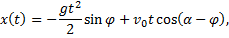
используя полученное выражение для 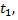имеем

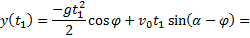
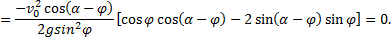
Поскольку по смыслу задачи 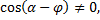то равно нулю выражение в квадратных скобках

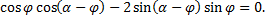
Отсюда после тригонометрических преобразований получаем

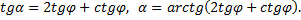
Рассмотрим пример. Человек, находящийся в точке 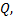движется вдоль оси ординат 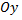в положительном направлении и тянет тяжелый предмет, расположенный в точке 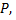за веревку постоянной длины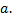

Пусть на плоскости 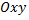в начальный момент времени точка 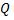находится в начале координат, а точка 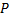имеет координаты 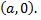Составим обыкновенное дифференциальное уравнение траектории точки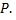

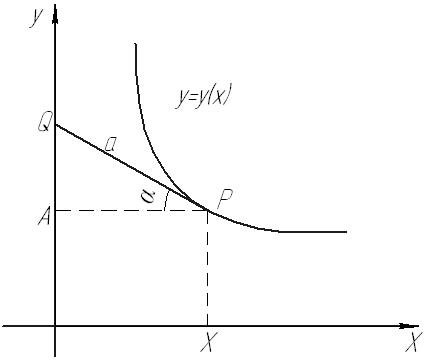
Рис. 65

Траектория точки

Обозначим через уравнение искомой траектории точки 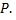Из условия задачи следует, что 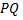является касательной к этой траектории в точке 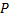с координатами 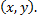Длина отрезк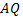а равна 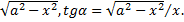Принимая во внимание геометрический смысл производной, т.е.

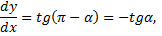
получаем обыкновенное дифференциальное уравнение первого порядка

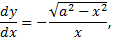
разрешенное относительно производной. Одним из решений этого дифференциального уравнения является функция, которая задает хорошо известную плоскую кривую – трактрису

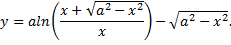
Рассмотрим пример. Сосуд, наполненный жидкостью, вращают с угловой скоростью вокруг оси Жидкость в сосуде образует воронкообразную полость, границей которой является поверхность вращения некоторой кривой, которая описывается уравнением 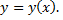Найдем форму этой поверхности.

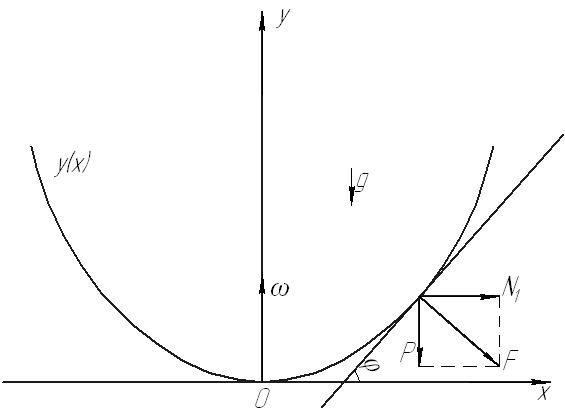
Рис. 66

Поверхность вращения кривой

Рассмотрим частицу на поверхности полости, имеющую массу и координаты 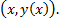Во вращающейся вместе с жидкостью системе координат 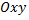частица покоится. В этом случае равнодействующая 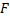силы тяжести 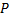и центробежной силы инерции 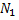с абсолютными значениями соответственно 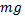и 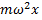ортогональна поверхности вращения. Тогда

Но в силу геометрической интерпретации производной 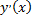как углового коэффициента касательной к графику функции 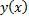имеем

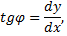
и поэтому

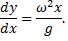
Решая это линейное однородное дифференциальное уравнение с начальным условием 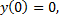получаем

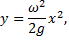
т.е. границей полости является параболоид вращения.

Рассмотрим пример. Составим дифференциальное уравнение, описывающее колебание некоторого конкретного маятника. Предельно идеализируя явление, считая, что движение происходит по прямой, пренебрегая сопротивлением среды, отвлекаясь от физических свойств маятника, получим дифференциальное уравнение

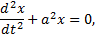
решение которого имеет вид

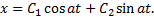
Это решение лишь грубо приближенно описывает явление.

Если учесть сопротивление среды и считать его пропорциональным скорости, то получим уравнение

Считая 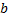малой величиной 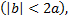получим следующее решение

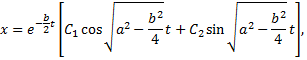
но и этот ответ является лишь довольно грубым приближением.

Если учесть, что движение происходит не по прямой, а по дуге окружности, то уравнение значительно усложнится и примет вид

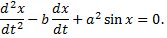
Данное уравнение лишь приближенно описывает процесс, в нем неточно учтен закон сопротивления среды и математический маятник рассматривается как материальная точка, не учтено действие возмущающих сил различного происхождения.

В этом примере, учитывая все новые и новые факторы, мы изменяли дифференциальное уравнение, описывающее изучаемое явление.

Дифференциальное уравнение, описывающее явление с учетом лишь основных, определяющих явление факторов, мало отличаются от дифференциальных уравнений, точно или хотя бы более точно описывающих тот же процесс.

Учитывая лишь основные факторы, мы исходим из предположения, что малое изменение уравнения лишь мало изменяет его решения.

Однако это основное предположение не всегда справедливо. Возьмем хотя бы уравнения

где постоянная величина 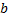мала. Сравним решения этих уравнений

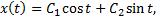
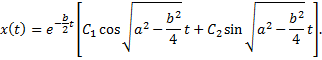
Для небольшого промежутка времени 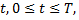решения этих двух уравнений, соответствующие одним и тем же начальным условиям, будут мало отличаться друг от друга, при достаточно малом 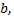но с возрастанием 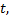как бы мало 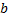ни было, решения этих уравнений все больше и больше будут отличаться друг от друга.

Решения первого уравнения периодические, решения же второго дают 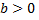затухающие колебания и при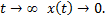

Если же 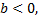то решения второго уравнения неограниченно возрастают по абсолютной величине при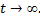

Таким образом, малое изменение правой части может даже качественно менять характер решения.

Решая конкретную задачу, мы ищем решение, удовлетворяющее определенным начальным условиям, однако эти начальные данные являются результатами некоторого измерения и вычисляются с некоторой погрешностью. Поэтому, можно пользоваться такими приближенными начальными данными только исходя из предположения, что малое изменение начальных данных незначительно изменит решение, т.е. решения непрерывно зависят от начальных данных.

Из всего выше сказанного можно сделать вывод: составив уравнение, описывающее какое-нибудь конкретное явление, необходимо помнить, что оно является лишь приближенным, что начальные данные, параметры и вид уравнения могут изменяться, если учесть ранее отброшенные факторы, или уточнить уже учтенные, или точнее измерить начальные данные и т.д.

Контрольные вопросы

1. В чем состоит особенность составления дифференциальных уравнений в прикладных задачах?

2. Привести примеры задач, приводящих к решению дифференциальных уравнений.