Нормальная система дифференциальных уравнений

Система вида

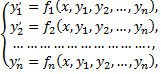
где функции 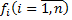определены в некоторой 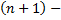мерной области переменных называется нормальной системой 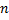дифференциальных уравнений первого порядка с неизвестными функциями

Число уравнений, входящих в систему, называется порядком нормальной системы. Решением нормальной системы в интервале 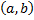называется совокупность функций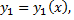

непрерывно дифференцируемых в интервале 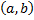и обращающих вместе со своими производными каждое уравнение нормальной системы в тождество.

Задача Коши для системы дифференциальных уравнений первого порядка имеет следующую формулировку. Найти решение 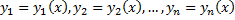нормальной системы дифференциальных уравнений первого порядка, удовлетворяющее начальным условиям 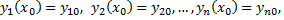где 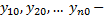заданные числа,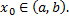

Теорема Коши о существовании и единственности решение задачи. Если функции 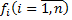непрерывны в окрестности точки и имеют непрерывные частные производные то всегда найдется некоторый интеграл с центром в котором существует единственное решение нормальной системы дифференциальных уравнений первого порядка, удовлетворяющее заданным начальным условиям.

Общим решением нормальной системы называется совокупность 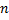функций

зависящих от произвольных постоянных 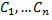и удовлетворяющих следующим условиям:

1) функции определены в некоторой области изменения переменных и имеют непрерывные частные производные

2) совокупность является решением нормальной системы дифференциальных уравнений первого порядка при любых значениях

3) для любых начальных условий из области 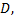где выполняются условия теоремы Коши, всегда найдутся такие значения произвольных постоянных 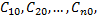что будут справедливы равенства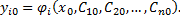

Частным решением нормальной системы дифференциальных уравнений первого порядка называется решение, полученное из общего при некоторых частных значениях произвольных постоянных.

Одним из методов решения нормальной системы дифференциальных уравнений первого порядка является сведение ее к решению одного или нескольких дифференциальных уравнений высших порядков – метод исключения.