Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнения вида

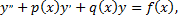
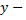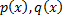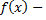где искомая функция, а и непрерывные функции на некотором интервале 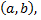называется линейным дифференциальным уравнением второго порядка.

Если 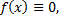то уравнение

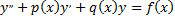
называется линейным однородным. Если 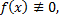то уравнение называется линейным неоднородным.

Разрешая данное уравнение относительно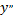

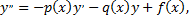
можно заметить, что оно является частным случаем уравнения и удовлетворяет условиям теоремы существования и единственности решения.

При отыскании общего и частного решений уравнений второго порядка важную роль играет понятие линейной зависимости и линейной независимости функций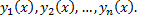

Функции называются линейно зависимыми в интервале 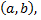если существуют постоянные числа 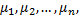не все равные нулю, такие, что

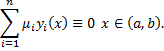
Если же указанное тождество выполняется, когда все 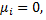то функции 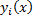называются линейно независимыми в интервале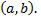

Критерий линейной независимости и линейной зависимости функций. Если функции 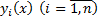в интервале 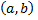(функции, имеющие в интервале 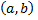непрерывные производные до 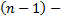го порядка включительно) линейно зависимы, то 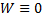в интервале 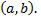Если 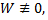то функции 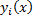линейно независимы, где 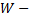определитель Вронского

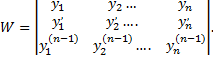
Если любая фундаментальная система решений уравнения

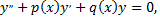
то функция

где 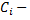произвольные постоянные, является общим решением уравнения

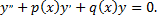
Фундаментальную систему уравнения

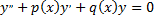
можно найти, используя только алгебраические методы, следующим образом.

Исходя из данного уравнения, составляют алгебраическое уравнение

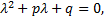
которое называется характеристическим уравнением для исходного. Оно имеет два корня, среди которых могут быть действительные простые и кратные корни, а также пары комплексно–сопряженных корней (простых и кратных).

Если корни характеристического уравнения действительные и различные 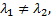то им соответствует фундаментальная система решений и общее решение уравнения

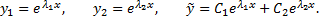
Если корни характеристического уравнения действительные и равные 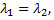то им соответствует

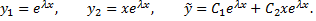
Если корни характеристического уравнения комплексно–сопряженные 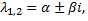то им соответствует

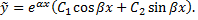
Рассмотрим пример. Найти общее решение дифференциального уравнения

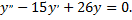
Составляем характеристическое уравнение, находим его корни, фундаментальную систему решений и общее решение уравнения

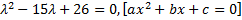
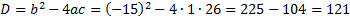
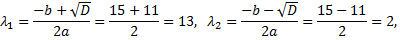
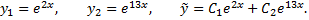
Рассмотрим пример. Найти общее решение дифференциального уравнения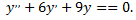

Составляем характеристическое уравнение, находим его корни, фундаментальную систему решений и общее решение уравнения

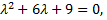
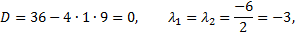
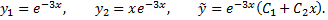
Рассмотрим пример. Найти общее решение дифференциального уравнения

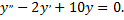
Составляем характеристическое уравнение, находим его корни, фундаментальную систему решений и общее решение уравнения

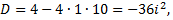
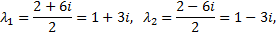
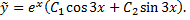
Контрольные вопросы

1. Сформулировать теорему Коши для дифференциального уравнения второго порядка.

2. Какое решение дифференциального уравнения второго порядка называют общим, а какое – частным?

3. Записать в общем виде линейное дифференциальное уравнения второго порядка с постоянными коэффициентами.

4. Какое уравнение называют характеристическим?