Анализ переходных процессов в цепи первого порядка.
2.1. Общий случай
 |
Цепь первого порядка с одним независимым источником описывается уравнением
 |
Записываем общее решение
Приравнивая правую часть в (1) к нулю, получим однородное уравнение
 |
 |
а затем из характеристического уравнения находим его корень
 |
то есть корень характеристического уравнения один и он обязательно отрицательный, что характерно для пассивной цепи. Величина обратная корню характеристического уравнения, взятого по модулю,
носит название постоянной времени.
 |
Записывая свободную составляющую в виде
 |
и подставляя (5) в (2) с учетом (4), имеем
 |
Решение (6) должно удовлетворять начальным значениям при t=0
 |
где х+уст - значение установившейся составляющей реакции в начальный момент, х+-начальное значение реакции. Откуда постоянная интегрирования
 |
Подставляя (8) в (6), записываем окончательно решение неоднородного дифференциального уравнения:
Таким образом определяется решение для любой цепи первого порядка. Как видно из (9), в цепи первого порядка переходный процесс полностью характеризуется постоянной времени.
Рассмотрим подробнее понятие постоянной времени цепи. Для этого рассчитаем и построим график кривой свободной реакции цепи первого порядка хсв, = Аеwt. В табл.2 приведены расчетные значения для конкретных значений времени t, кратных постоянной времени т, а на рис.2.1 в соответствии с данными табл.2 построен график сводной реакции.
Таблица 2
| t | 1t | 2t | 3t | 4t | |
| e-t/t | 0.368 | 0.87 | 0.95 | 0.98 | |
| 1- e-t/t | 0.632 | 0.13 | 0.05 | 0.02 |
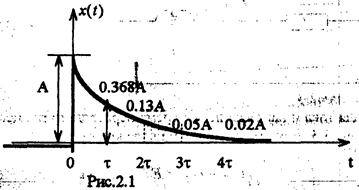
Как видно из рис 2.1 и табл.2, при t=3t сводная реакция составляет 0.05А (5%) от начального значения ,при t=4t -0.02A (2%) от начального значения, т.е. с погрешностью 5% для первого случая и 2% для второго случая можно считать, что сводная составляющая равна нулю и в цели имеет место установившейся режим работы. Поэтому постоянная времени характеризует длительность переходного процесса. Теоретически переходный пороцесс продолжается бесконечно долго, реально длительность переходного процесса Tnn
принимается равной 3-4 t, Tnn @(3-4)t.
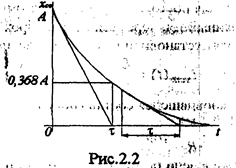
Так как отрезок подкасательной в любой точке кривой Ае –t/t равен постоянной величине t (см. рис: 2.1) и имеет размерность времени, то значение величины t определяет скорость затухания свободной реакции, т.е. скорость изменения тока или напряжения во время переходного процесса. Экспериментально постоянная времени t определяется либо как абсцисса точки на кривой сводной реакции (рис 2.2), ордината которой равна 0.368А, либо как отрезок , отсекаемый подкасательной на оси абсцисс подкасательной, г. с. постоянная времени численно равна отрезку времени в течении; которого ток либо напряжение изменяются в е раз. Итак ,в цепи первого порядка вид и длительность переходного процесса полностью определяется постоянной времени t. Причем при включении цепи одной и той же топологии (конфигурации) на источник постоянного или переменного, гармонического напряжения постоянная времени одна и таже, так как является величиной, обратной корню характеристического уравнения, взятому по модулю.
Рассмотрим конкретные случаи переходных процессов в цепи первого порядка.
2.2. Включение цепи RL на источник постоянного напряжения
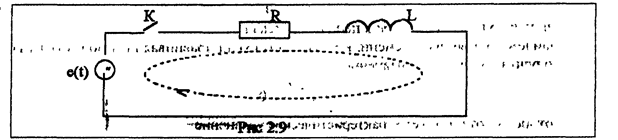
Определим закон изменения тока и напряжения во время переходного процесса в цепи, изображенной на рис.3.3. Для этого для цепи после коммутации составим уравнение по ЗНК.
Будем иметь:
 |
общее решение в соответствии с выражением (9) раздела 3.1, имеет вид:
 |
Найдем установившуюся составляющую тока. Для этого составим эквивалентную расчетную схему для цели в новом установившемся режиме работы. Если источник постоянный, то необходимо закоротигь ветви с индуктивностями ( ul=o для постоянного тока) и разомкнуть ветви с емкостями( ic=0 -постоянный ток через емкость не проходит); из расчета полученной схемы находят установившуюся составляющую.
 |
Начальное значение установившейся составляющей
 |
Начальное значение тока в цепи по закону коммутации
так как до коммутации ток в цепи не протекал.
 |
Найдем постоянную времени цепи для данного случая. Характеристическое уравнение имеет вид
Откуда постоянная времени для цепи с индуктивностью
 |
 |
Исходя из (3) с учетом (4)-(6), (8), записываем окончательно выражение для тока (реакции) во время переходного процесса
| или |
Найдем изменение напряжения на индуктивности

В соответствии с полученными выражениями на рис 2.4а,б построены зависимости тока и напряжения индуктивности во время переходного процесса при включении цепи RL на источник постоянного напряжения.
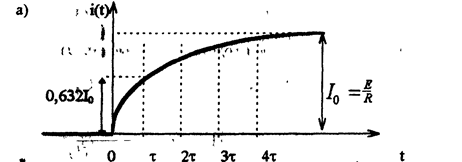
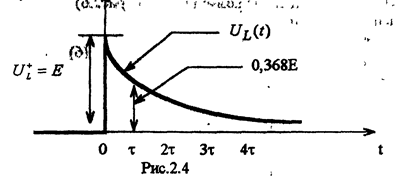
Ток и напряжение изменяются по экспоненциальным законам. При этом, ток индуктивности изменяется непрерывно, а напряжение индуктивности в момент коммутации имеет скачок напряжения U+L=E, равный напряжению источника. Постоянная времени может быть найдена по кривой тока (возрастающей экспоненциальной зависимости) как абсцисса точки, ордината которой равна 0,632Iо от установившегося значения тока.
Для убывающей экспоненциальной зависимости -как абсцисса точки, ордината которой равна 0,368 от начального значения.
2.3 ???
 |
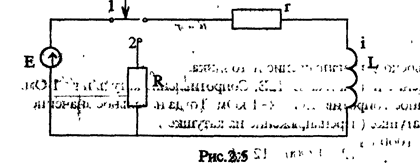
Во время коммутации ключ переводится из положения 1 в 2 т.е цепь. отключается от источника и замыкается на добавочное сопротивление R. Для цепи после коммутации уравнение по ЗНК имеет вид.
| или |

т.е. получили однородное дифференциальное уравнение с постоянными коэффициентами. Как известно, общее решение записывается в следующем виде
(производную di/dt заменяем на a)

Составим характеристическое уравнение

откуда

Из закона коммутации с учетом схемы цепи до коммутации (см. рис2.б) начальное значение тока в цепи (при t=0)
 |
Так как в новом установившемся режиме цепь отключена от источника, то установившаяся составляющая реакции равна нулю iycт=O, поэтому также начальное значение установившейся составляющей iyст = 0 С учетом (6) общее решение (3) имеет вид
При этом напряжение
Как видно из рис.2.7, во время коммутации напряжение на индуктивности имеет
 |
1 скачок напряжения ( перенапряжение)
, которое может значительно превосходить напряжение источника.
Пример. Напряжение источника Е=12В. Сопротивление катушки r= 1 Ом.
 |
Добавочное сопротивление R=1 кОм. Тогда начальное значение напряжения на катушке (перенапряжение на катушке)
Такое напряжение может привести к пробою межвитковой изоляции, вызвать межвитковое короткое замыкание, искрение контактов переключателя, горение дуги, т.е. привести к аварийному режиму работы. Поэтому при отключении больших индуктивностей необходимо предусмотреть меры по снижению начального перенапряжения на индуктивности реостатное выключение, шунтирование индуктивности гасящими цепочками (см.рис.2.8 ) 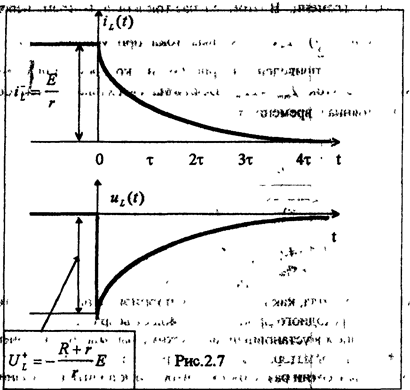
2.4 Переходный процесс в цепи RL при включении на синусоидальное напряжение
 |
Пусть напряжение источника изменяется по следующему закону
 |
где y-начальная фаза, определяющая момент коммутации и называемая фазой включения. В этом случае по-прежнему начальное значение тока
 |
а установившиеся значения тока определяется
 |
где j=arctg(wL/R) - угол сдвига между током и напряжением. Тогда подставляя найденные значения в общее решение для цепи первого порядка (3) предыдущего раздела получим
 |
Вид переходного процесса в этом случае определяется не только постоянной времени, но и существенно зависит от фазы включения y. Если y-j=0, то свободный ток iсв(t)=Imsin(y-j)e-t/t =0 и переходный процесс отсутствует, сразу после включения наступает установившейся режим. если же y-j=p/2, то iсв(t)=Imet/t имеет наибольшее значение в начальный момент времени. В этом случае ток в цепи во время переходного процесса
 |
Кривая тока при условии, что
имеет, приведена на рис.2.6, из которого видно, что в цепи образуется сверхток Imm £2Im. Величина сверхтока Imm тем больше, чем больше постоянная времени t.
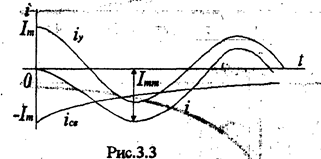
Электродинамическая сила, как известно, пропорциональна квадрату тока. Поэтому во время переходного процесса она может возрасти до 4 раз по сравнению со значением в установившемся режиме работы. Для нелинейной индуктивности (трансформатора) сверхток возрастает в десятки раз, следовательно, силы в сотни раз. Поэтому, чтобы исключить их механические повреждения, необходим бандаж для обмоток и для магнитопровода (стяжки).
Пепреходный процесс в цепи RL при включении на синусоидальное напряжение
 |
Пусть напряжение источника на входе цепи (рис 2.9) изменяется по следующему закону
 |
где y-начальная фаза, определяющая момент коммутации и называемая фазой включения. В соответствии с ЗНК, составленного для цепи после коммутации, имеем неоднородное дифференциальное уравнение первого порядка
 |
либо в нормальной форме
 |
Как известно можно записать
Установившеюся составляющую тока найдем из расчета цепи (см. рис 2.10) на основе метода комплексных амплитуд.
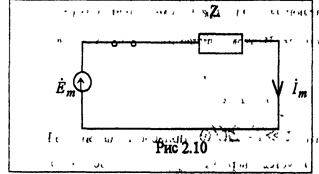
 |
По закону Ома:
 |
Где комплексное сопротивление цепи

Исходя из (4), записываем мгновенное значение установившегося тока

и значение установившейся составляющей при t=0

В соответствии с законом коммутации ток индуктивности скачком измениться не может, поэтому начальное значение тока в цепи
так как до коммутации ток в цепи не протекал.

Найдем постоянную времени. Из уравнения (3) .приравнивая правую часть нулю, получим однородное уравнение

которому соответствует характеристическое уравнение

Откуда постоянная времени

Записывая окончательно решение уравнения в соответствии с выражением (3) и с учетом (10),(7),(б),(5) будем иметь.

Вид переходного процесса в этом случае отделяется не то времени, но и существенно зависит от фазы включения y. Если y- j = 0, то свободный ток

и переходный процесс отсутствует, сразу после включения наступает установившейся режим.

то свободная составляющая

имеет наибольшее значение в начальный момент времени. В этом случае ток в цепи во время переходного процесса
Кривая тока при условии, что t»T=2p/w, приведена на рис.2.11, из которого видно, что в цепи образуется сверхток Imm£2Im. Величина сверхтока Imm тем больше, чем больше постоянная времени t.
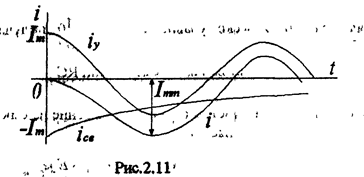
Электродинамическая сила, как известно, пропорциональна квадрату тока. Поэтому во время переходного процесса она может возрасти до 4 раз по сравнения со значением в установившемся режиме работы. Для нелинейной индуктивности (трансформатора) сверхток возрастает в десятки раз, следовательно, силы в сотни раз. Поэтому, чтобы исключить механические повреждения обмоток и шихтованного магнитопровода, необходим бандаж для обмоток и для магнитопровода (стяжки). Мощные трансформаторы (индуктивности) включают при фазе включения y- j = 0,, чтобы отсутствовал переходный процесс и сразу наступал установившейся режим работы.
2.5 Включение цепи RС на постоянном напряжении
В соответствии ЗНК iR +Uc = Е и учитывая, что ток I = С(dUc)/dt имеем следующее неоднородное дифференциальное уравнение для цепи

или в нормальной форме

Общее решение запишем в следующем виде

Напряжение на емкости в новом установившемся режиме и его значение при t=0 равны, соответственно
В соответствии с законом коммутации напряжение емкости во время коммутации
скачком измениться не может, поэтому

т.е. пусть до коммутации на емкости имелось начальное значение Uo.

Составляя характеристическое уравнение получаем

Постоянная цепи RC:

В соответствии с (3) и с учетом (4) - (6) напряжение на емкости во время переходного процесса изменяется

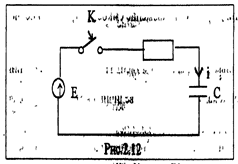
На рис. 2.13. в соответствии с (7) и (8) построены напряжение емкости и ток в цепи для трех случаев в зависимости от начального напряжения емкости.
1-й случай. Заряд емкости: Пусть напряжение Uo=0, из выражений (7) и (8)
2-й случай. Дозаряд емкости: Начальное напряжение емкости 0 < Uо < E тогда напряжение и ток изменяются в соответствии с выражениями (7) и (8). При этом как видно из выражения (8), ток при дозаряде минимальный.
3-й случай перезаряд емкости : Uо < 0 напряжение емкости отрицательное но по модулю IUoI < Е
Как видно полученных кривых, в начальный момент времени при включении цепи RC имеет место скачок тока, i+=-(Uo-E)/R , величина которого значением источника ЭДС E, начальным напряжением на емкости Uo и активным сопротивлением цепи R. При этом наибольшее значение скачок тока имеет место при перезаряде емкости, что необходимо учитывать при включении конденсаторов ( необходимо подключать сопротивления, ограничивающие ток заряда емкости).
Перенапряжений ЗАМЕЧАНИЕ
Если рассмотреть энергетические процессы при включении цепи RC на источник постоянного напряжения, то окажется, что за время переходного процесса 50% энергии источника выделяется на активном сопротивлении в виде тепла, а 50% запасается в виде энергии электрического поля емкости, т.е. КПД такого устройства 50 %. Другими словами, если необходимо запасти в конденсаторе энергию 1 Дж, то от источника будет потреблена энергия в 2 Дж, энергия в 1Дж будет выделена в виде потерь на соединительных проводах.
|
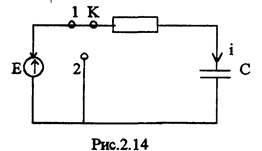
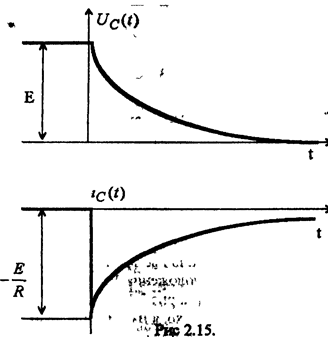
2.6 Коротеое замыкание цепи RC
Ключ во время коммутации из положения 1 переводится в 2 (см рис 2.14). Исходя из ЗНК для цепи после коммутации, iR + U с = О дифференциальное уравнение относительно напряжения емкости имеет вид:

Составляя характеристическое уравнение
 |
и определяя его корень, найдем постоянную времени цепи RC
В соответствии с законом коммутации начальное напряжение на емкости U+c=U-c; = E. Так как после коммутации цепь отключается от источника, то установившиеся напряжение Uс.уст (t) == U+c.ycrn = S . Теперь, исходя из общего решения (см. выражение (3) раздела 2.5.), окончательно записываем решение 
дифференциального уравнения и находим ток цепи.
Как видно из полученныхкривых, процесс закорачивания цепи RC является неопасным режимом работы. Если рассматривать энергетические процессы в цепи, то окажется, чтоза время переходного процесса энергия накопленная в электрическом поле емкости к моменту коммутации полностью выделяется в виде тепла на активном сопротивлении.
|
2.7. Включение цепи RC на источник гармонического напряжения
Пусть исследуемая цель RС включается под действием гармонического источника е(t)=Emsin(wt+y) при нулевых начальных условиях Uc == 0. Дифференциальное, уравнение составленное по ЗНК Ri+Uc =e(t), представим в виде (dUc)/dt=-1/(RC)Uc+1/Ce(t), затем составляем характеристическое 
уравнение a+1/(RC)=0 и находим постоянную времени

В соответствии с (3) раздела 2.
так как по закону коммутации напряжений U+C=UC-= 0.

При синусоидальном напряжении источника
установившейся ток
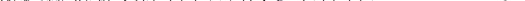
, где j=arctg(wRC)-1 - угол сдвига между током и напряжением источника, а установившиеся напряжение

где амплитудное напряжение на емкости

Тогда из выражения 1) с учетом (2) (3) имеем
Вид переходного процесса зависит от фазы включения Y. Если Y-j=p/2

то свободная составляющая напряжения емкости

и переходный процесс отсутствует. При Y-j=0 UСсв имеет наибольшее значение и напряжение и ток имеют следующие выражения
На рис.2.16,а приведена кривая UС(t) при t³2p/w из которой видно что на емкости в этом случае возникает перенапряжение. При малой постоянной времени ( t « 2p/w) в цепи в начальный Момент времени возникает значительный бросок тока величиной I(0)= - Im/(wt) (рис.2.16,6), который может
Дата добавления: 2015-08-21; просмотров: 3491;
