Действующее значение и мощность в цепе несинусоидального тока.

Рассмотрим действующие значения тока , напряжения и ЭДС на примере действующего значения тока.

Пусть ток разложен в ряд Фурье:

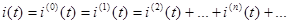
Как известно, действующее значение периодического тока (синусоидального и несинусоидального) определяется его средне квадратичным значением

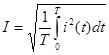
где Т-период несинусоидалъного тока.

Для определения действующего значения необходимо ряд возвести во вторую степень. При возведения ряда во вторую степень результат может быть представлен

виде двух сумм. Например для трех слагаемых a1, a2, a3 имеем:

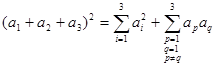
С учетом последнего будем иметь для действующего значения тока

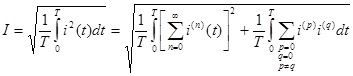
Поменяем местами порядок суммирования и интегрирования, получим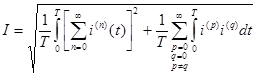

Рассмотрим произведение'р ' -ой гармоники на'q' -ую гармонику . В < ортогональности функции 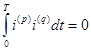т.е. вторая сумма под радикалом равна нулю.

При этом первая сумма равна

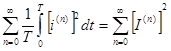
где 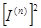-квадрат действующего значения'n' -ой гармоники

Из выше перечисленного следует , что действующее значение несинусоидильного тока равно корню из суммы квадратов действующих значений каждой из гармоник в отдельности, включая и постоянную составляющую.

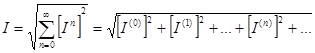(4.4)

Аналогично выражается действующее значение напряжения и ЭДС. Пример: Найдем действующее значение тока , заданного следующим выражением:

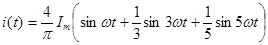
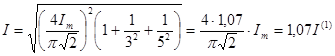
Т.е. в действующем значении удельный вес высших гармоник незначителен , поэтому для приближенных расчетов часто используется расчет по основной (1-ой гармонике) (см. Нелинейные цепи: Метод эквивалентных синусоид).