Расчет цепей при периодическом воздействии.

Рассмотрим двухполюсник на входе которого действует исто^чник несинусоидальной э.д.с , представленной рядом Фурье:

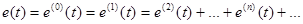
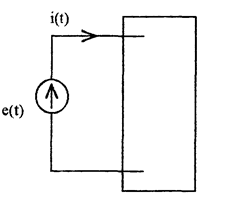
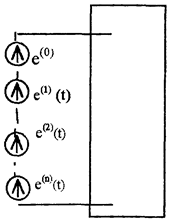
Так как цепь линейная то при расчете тока можем воспользоваться принципом наложения ,из которого следует, что если в электрической цепи действует несколько источников э.д.с (токов), то ток в цепи равен соответствующей сумме частичных токов, вызванных каждым из источников в отдельности

Рис 43

В соответствии с принципом наложения рассмотрим один источник (например e(0) те постоянную составляющую), а все остальные источники закоротv

рассчитаем ток постоянной составляющей i(0) В схеме при этом ивдуктивность ( закорачиваются , а емкости размыкаются , т.к. ток постоянный не проходит через емкость, а напряжение на индуктивности нулевое

Далее рассчитываем цепь при действии 1-ой гармоники (выполняется методом комплексных амплитуд). Аналогичный расчет'n' -ой гармоники , при этом сопротивление реактивных элементов схемы отличается в'n' раз : сопротивление

индуктивности возрастает, а сопротивление емкости уменьшается в 'n' раз по сравнению с сопротивлением для 1-ой гармоники:

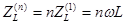
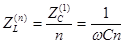
В итоге ток равен сумме частичных токов :

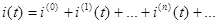
Рассмотрим более подробно влияние характера цепи на форму токов и

напряжений , т е. рассмотрим отношение действующих значений'k '-ой гармоники тока к основной:

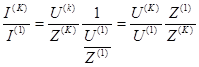
1 случай. Пусть сопротивлением нагрузки является активное сопротивление R Тогда:

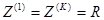
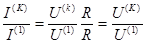
Следовательно в цепи с активным сопротивлением формы кривых тока и напряжения одинаковы.

2 случай. В качестве нагрузки возьмем индуктивность L

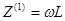
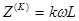
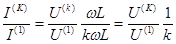
Так как относительная величена'К ' -ой гармоники тока в'k' раз мен

относительной величены напряжения'k' -ой гармоники, т.е. говорят, индуктивность сглаживает ток .(широко используется в фильтрах(см ниже))

3 случай. В качестве нагрузки емкость С .

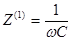
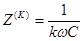
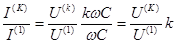
4 случай. Последовательный контур L-C :

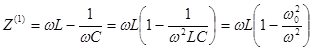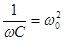где -квадрат резанансной частоты.

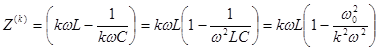
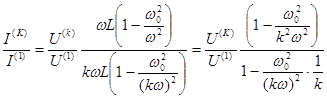
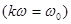,то ‘k’-ая

Если имеется резонанс на частоте 'К' -ой гармоники

гармоника тока стремится к бесконечности . (Хорошо для выделения гармоники . Используется в полосовом фильтре.)

5 случай . Параллельный контур L-C :

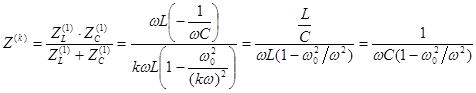
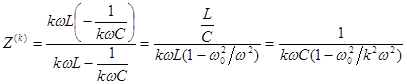
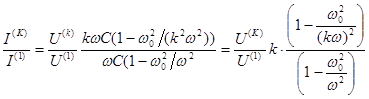
На частоте 'К' -той гармоники , равной резонансной частоте

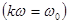данное отношение стремится к нулю. Поэтому'k' -тая гармоника тока

не пропускается, задерживается двухполюсником (используется в заграждающих фильтрах пробках).