Функция нечетная
(симметрична относительно начала коордюат) f(t)= -f(-t). Отсутствуют косинусоидальные гармоники и постоянная составляющая
аn=О
З.Функция симметрична относительно оси абсцисс со
cдвигом за период 
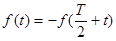
| Отсутствуют гармоники с четными порядковыми номерами. |
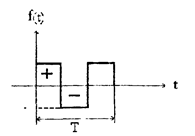
На практике могут быть комбинации рассмотренных случаев . 1и3: 2и3 На I рис 4.2 для примера представлена диаграмма разложения прямоугольных разнополярных импульсов в ряд Фурье согласно выражению 4 1
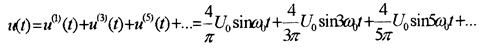
| Так как функция обладает 1 и 3 видами симметрии, то в разложении присутствуют синусоидальные гармоники с нечетными порядковыми номерами (см. рис 4.2). |
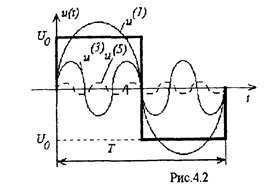
При анализе цепей несинусоидального тока удобно гармонический состав тока (напряжения, ЭДС ) представлять в виде амплитудного и фазового дискретных
( линейчатых ) спектров.
Под амплитудном линейчатым спектром понимают зависимость амплитуды тока (напряжения, ЭДС ) от частоты (порядкового номера гармоники).
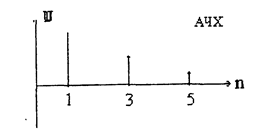
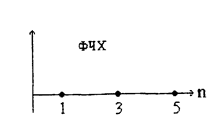
Под фазовым линейчатым спектром понимают зависимость фазы тока ( напряжения ) от частоты (порядкового номера). На рисунках показаны соответствующие амплитудный (АЧХ) и фазовый (ФЧХ) дискретные спектры.
|
|
Амплитудные значения 1,3,5 гармоник и их начальные фазы при этом равны соответственно
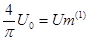
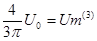
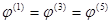
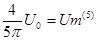
Дата добавления: 2015-08-21; просмотров: 1029;
